
(7分)在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.

(1)求证: ;
;
(2)若 ,求
,求 的度数.
的度数.
(1)Rt△ABE≌Rt△CBF;(2)∠ACF=30°.
【解析】
思路点拨:(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可证Rt△ABE≌Rt△CBF;
(2)由等腰直角三角形的性质易求∠BAE=∠CAE-∠CAB=15°,得到∠BAE=∠BCF=15°,进而求得∠ACF的度数.
试题分析:(1)证明:在Rt△ABE和Rt△CBF中,
∵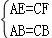 ,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)如图,∵在△ABC中,AB=CB,∠ABC=90°,
∴∠ACB=∠CAB=45°,
∴∠BAE=∠CAE﹣∠CAB=15°.
又由(1)知,Rt△ABE≌Rt△CBF,
∴∠BAE=∠BCF=15°,
∴∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°.
考点:全等三角形的判定与性质;等腰直角三角形的性质


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源:2014-2015学年江苏省启东市八年级12月月考数学试卷(解析版) 题型:解答题
已知:a,b,c为△ABC的三边长,且a2+b2+c2=ab+ac+bc,试判断△ABC的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市八年级12月月考数学试卷(解析版) 题型:选择题
把(-2)2014+(-2)2015分解因式的结果是( ).
A.22015 B.-2 2015 C.-2 2014 D.22014
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中考试数学试卷(解析版) 题型:填空题
在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为40°,则
∠B= _____________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县七年级上学期期中联考数学试卷(解析版) 题型:解答题
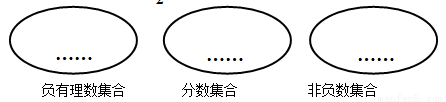
把下列各数填在相应的集合圈里:(每个空格2分,共6分)
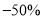 ,0.628,-3,
,0.628,-3,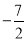 ,0,
,0,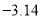 ,5.9,
,5.9,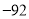
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com