
����Ŀ������������仭ͼ�����ش���Ӧ���⣺��֪����AOB��
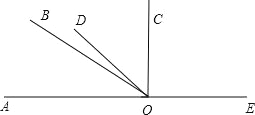
(1)������ OA �ķ����ӳ��� OE��
(2)���������� OC��ʹ��AOC=90�㣻
(3)������ OD��ʹ��COD=��AOB��
(4)ͼ�й��� ������������ƽ�ǣ�
(5)����� ���۽��� ��ֱ���� ��ƽ���� ��
(6)�����ҳ�ͼ��������ȵĽ��𣨳���COD=��AOB �⣩�����ܶ�д������
(7)���COD ����Ľ��� ���������Ľ��� ����

���𰸡�(1)��(2)��(3)��ͼ�������� (4)10��(5)��AOB����AOD����BOD����BOC����DOC����BOE����DOE����AOC����COE����AOE�� (6)��AOC=��COE=90�㣻��AOD=��BOC��(7)1��2.
��������
���ݽǵĸ����һ�������������ߵ�ͼ�νнǣ�����90�ȵĽǽ�ֱ�ǣ�����0��С90�ȵĽǽ���ǣ�����90��С��180�ȵĽǽж۽ǣ�180�ȵĽǽ�ƽ�ǣ����ǵĺ�Ϊ90�ȵĽǻ�Ϊ��ǣ����ǵĺ�Ϊ180�ȵĽǻ�Ϊ���ǣ�
(1)(2)(3)��ͼ��
(4)�� 5 �����ߣ��ǵĸ���=4��5��2=10 ����
(5)����С�AOB����AOD����BOD����BOC����DOC�� �۽��С�BOE����DOE��ֱ���С�AOC����COE�� ƽ���С�AOE��
(6)��AOC=��COE=90�㣻��AOD=��BOC��
(7)��COD �������AOD��
�ߡ�COD=��AOB��
��AOB ���BOE ������
���COD ���BOE �����������COD����Ľ���1�������COD�����Ľ���2��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����D��EΪ��O��λ��AB�������㣬����BD���ӳ�����C��ʹ��CD=BD������AC����O�ڵ�F������AE��DE��DF��
��1��֤������E=��C��
��2������E=55�㣬���BDF�Ķ�����
��3����DE��AB�ڵ�G����DF=4��cosB= ![]() ��E��
��E�� ![]() ���е㣬��EGED��ֵ��
���е㣬��EGED��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���Ա�ʾΪ���������������̵���ʽ������Ϊ���������������Կ�����ĸΪ1������������֮Ϊ������.��![]() ���ܱ�ʾΪ�������ʵ��������̣�����
���ܱ�ʾΪ�������ʵ��������̣�����![]() ������������.��������֤����
������������.��������֤����
��![]() ��a��b�ǻ��ʵ�������������b��0����2=
��a��b�ǻ��ʵ�������������b��0����2=![]() ������a=2b.
������a=2b.
��Ϊb�������Ҳ�Ϊ0������a�Dz�Ϊ0��ż��.��a=2n��n����������
����b=2n������bҲ��ż������a��b�ǻ��ʵ�����ì�ܣ�
����![]() ��������.
��������.
��ϸ�Ķ����ģ�Ȼ����֤����![]() ����������
����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ��� y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����������ĸ����ۣ� ��abc=0����a+b+c��0����a��b����4ac��b2��0�� ������ȷ�Ľ����У� ��
A.1 ��
B.2 ��
C.3 ��
D.4 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCֽƬ��DE�۵���ʹ��A���ڵ�A'������A'Bƽ�֡�ABC��A'Cƽ�֡�ACB������BA'C=110�������1+��2�Ķ���Ϊ��������

A. 80�㣻 B. 90�㣻 C. 100�㣻 D. 110�㣻
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=60�㣬��ABC����ACB��ƽ���߽���E��D��AE�ӳ�����һ�㣬�ҡ�BDC=120�������н��ۣ��١�BEC=120�㣻��DB=DE���ۡ�BDE=2��BCE��������ȷ���۵ĸ���Ϊ��������

A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��3x��3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=x2+bx+c����A��C���㣬����x�ύ����һ��B����B�ڵ�A�Ҳࣩ��
��1���������ߵĽ���ʽ����B���ꣻ
��2������M���߶�BC��һ���㣬����M��ֱ��EFƽ��y�ύx���ڵ�F�����������ڵ�E����ME�������ֵ��
��3����̽����MEȡ���ֵʱ����x���·����������Ƿ���ڵ�P��ʹ��M��F��B��PΪ������ı�����ƽ���ı��Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��k��0���뷴��������y= ![]() ��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1��
��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1�� 
��1�����������Ľ���ʽ��
��2������OB��O������ԭ�㣩������BOC�����Ϊ3�����һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����б�����Ĺ�ϵ���Ǻ�����ϵ���ǣ�������
A. �����εĿ�һ�����䳤�����
B. �����ε��ܳ������
C. ���������εĵױ߳������
D. Բ���ܳ���뾶
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com