解:(1)(-

)
4005×16
2003
=(-

)
4005×(4
2)
2003=(-

)
4005×4
4006
=(-

)
4005×4
4005×4
=[(-

)×4]
4005×4
=(-1)×4
=-4;
(2)3
18×(-

)
8=3
18×[-(

)
2]
8
=3
18×(

)
16=3
16+2×(

)
16
=(3×

)
16×3
2
=9;
(3)(0.5×3

)
199•(-2×
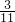
)
200=(0.5×

)
199•(-2×
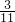
)
200=[0.5×

×(-2)×
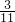
]
199×(-2×
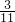
)
=
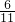
;
(4)0.25
9×2
20×25
9×64
3
=0.25
9×64
3×2
20×25
9=0.25
9×(4
3)
3×4
10×25
9
=(0.25×4)
9×(4×25)
9×4
=4×10
18.
分析:(1)由于16
2003=(4
2)
2003=4
4006,再逆用同底数幂、积的乘方的运算性质,并且结合乘法的交换律、结合律简便计算;
(2)由于(-

)
8=[-(

)
2]
8=(

)
16,再逆用同底数幂、积的乘方的运算性质,并且结合乘法的交换律、结合律简便计算;
(3)先逆用同底数幂的运算性质,将(-2×
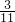
)
200改写成(-2×
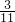
)
199×(-2×
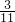
),再逆用积的乘方的运算性质求解;
(4)由于2
20=(2
2)
10=4
10,64
3=(4
3)
3=4
9,再逆用同底数幂、积的乘方的运算性质,并且结合乘法的交换律、结合律简便计算.
点评:解题关键是掌握同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加.

 )4005×162003=______;
)4005×162003=______; )8=______;
)8=______; )199•(-2×
)199•(-2×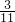 )200=______;
)200=______; )4005×162003
)4005×162003 )4005×(42)2003
)4005×(42)2003 )4005×44006
)4005×44006 )4005×44005×4
)4005×44005×4 )×4]4005×4
)×4]4005×4 )8
)8 )2]8
)2]8 )16
)16 )16
)16 )16×32
)16×32 )199•(-2×
)199•(-2×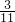 )200
)200 )199•(-2×
)199•(-2×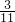 )200
)200 ×(-2)×
×(-2)×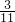 ]199×(-2×
]199×(-2×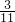 )
)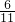 ;
; )8=[-(
)8=[-( )2]8=(
)2]8=( )16,再逆用同底数幂、积的乘方的运算性质,并且结合乘法的交换律、结合律简便计算;
)16,再逆用同底数幂、积的乘方的运算性质,并且结合乘法的交换律、结合律简便计算;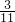 )200改写成(-2×
)200改写成(-2×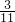 )199×(-2×
)199×(-2×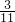 ),再逆用积的乘方的运算性质求解;
),再逆用积的乘方的运算性质求解;

 阅读快车系列答案
阅读快车系列答案