
����Ŀ����һ����ֱ�Ĺ�·����A��B����.�ס�������ͬʱ����,����綯����A�ص�B��,��;���ֹ��Ϻ�ͣ��ά��,�ó�����ԭ�ټ�����ʻ��B��;����Ħ�г���B�ص�A��,����A�غ�������ԭԭ�ٷ���,�������ͬʱ��B��.��ͼ�Ǽס���������B�صľ���y(km)������ʻʱ��x(h)֮��ĺ���ͼ��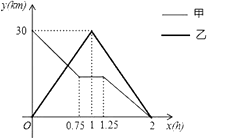
��1��A��B���ؼ�ľ���Ϊkm��
��2��������B�صľ���y(km)������ʻʱ��x(h)֮��ĺ�����ϵʽ��
��3����ס��ҵ�һ��������ʱ�䣻
��4��������֮��ľ��벻����10kmʱ,�ܹ������߶Խ���������ϵ,����������н����������߶Խ�����ױ�����ϵ��xȡֵ��Χ��
���𰸡�
��1��30
��2������ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1=k1x�������⣬��
30=k1��
��y��1=30x
���ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2=k2x+b2�������⣬��![]()
��ã�![]()
����y=-30x+60
��3���ɺ���ͼ��
��30+20��x=30��
���x=0.6��
��ס��ҵ�һ���������ڳ�����0.6Сʱ
��4��
������ǰy��x֮��ĺ�����ϵʽΪy��1=kx+b�������⣬�ã�![]()
��ã�![]()
y��1=-20x+30��
���������y��x֮��ĺ�����ϵʽΪy��2=k3x+b3�������⣬��![]()
��ã�![]()
��y��2=-20x+40��![]()
��ã�![]()
����ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1=k1x�������⣬��![]()
���ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2=k2x+b2�������⣬![]()
��y=-30x+60��
��![]() ʱ
ʱ
��![]()
![]()
![]()
���������⣺��1����ͼ����y��ļ׳�ʼֵ��30����֪A��B���ؼ�ľ���Ϊ30ǧ��
��1���ɺ���ͼ������������ʻ��ʱ�䣬�Ϳ�����·�̡�ʱ���������ʻ���ٶȣ�
��2�����������⼴Ϊ��ֱ���ཻ���⣻
��3���������ǰy��x֮��ĺ�����ϵʽΪy��1=kx+b����������y��x֮��ĺ�����ϵʽΪy��2=k3x+b3����ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1=k1x�����ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2=k2x+b2���ɴ���ϵ�����������ʽ��������ʽ�������⼴�ɽ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼���������¼����ǣ�������
A. Ͷ��ö���ӣ��泯�ϵĵ���֮��Ϊ7
B. �����������β�Ʊ�����д�
C. Ͷ��öӲ�ң����ϵ����Ϊ����
D. NBA�˶�Ա����Ͷ�����ξ�δ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�ڣ���A��n��n��1��һ�����ڣ�������
A. ��һ����B. �ڶ�����C. ��������D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2000��ƻ������ȡ100���������в������2����������2000��ƻ�����в���ĸ���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=![]() x��6�ֱ�x�ᣬy����A��B��M�Ƿ���������y=
x��6�ֱ�x�ᣬy����A��B��M�Ƿ���������y=![]() ��x��0����ͼ����λ��ֱ���Ϸ���һ�㣬MC��x�ύAB��C��MD��MC��AB��D��ACBD=4
��x��0����ͼ����λ��ֱ���Ϸ���һ�㣬MC��x�ύAB��C��MD��MC��AB��D��ACBD=4![]() ����k��ֵΪ�� ��
����k��ֵΪ�� ��
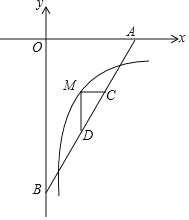
A����3 B����4 C����5 D����6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5��14��15�ա�һ��һ·����̳����ڱ���¡���ٿ����ٽ����ҹ�����������Ļ�����ͨ���ݣ���һ��һ·����������������ԼΪ44���ˣ�44��������ÿ�ѧ��������ʾΪ�� ��
A.4.4��108
B.4.4��109
C.4��109
D.44��108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������֮��һ���Ƕ۽�����_____������������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨�����������һԪ���η���![]() ������ʵ������������һ��������һ������2������������ķ���Ϊ������������.�������н��ۣ�
������ʵ������������һ��������һ������2������������ķ���Ϊ������������.�������н��ۣ�
������![]() �DZ������̣�
�DZ������̣�
���������ķ���![]() �DZ������̣���a=��3��
�DZ������̣���a=��3��
��������x�ķ���![]() �DZ������̣���������
�DZ������̣���������![]() ��x��Ĺ������������(2,0)�ͣ�4,0����
��x��Ĺ������������(2,0)�ͣ�4,0����
�����㣨m��n���ڷ���������![]() ��ͼ���ϣ������x�ķ���
��ͼ���ϣ������x�ķ���![]() �DZ�������
�DZ�������
������������ȷ���У� ��
A.���� B.���� C.���� D.����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com