
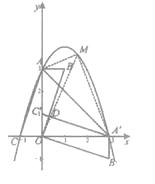
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
【答案】
(1)
解:∵□A′B′OC′由□ABOC旋转得到,且点A的坐标为(0,3),
点A′的坐标为(3,0).
∴抛物线过点C(-1,0),A(0,3),A′(3,0),
设抛物线的解析式为y=ax2+bx+c(a≠0),可得
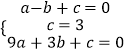 解得
解得 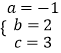
∴过点C,A,A′的抛物线的解析式为y=-x2+2x+3.
(2)
解:∵AB//CO,∴∠OAB=∠AOC=90°,
∴OB= ![]() ,
,
又∠OC′D=∠OCA=∠B,
∠C′OD=∠BOA,∴△C′OD~△BOA,
又OC′=OC=1,
∴ ![]() ,
,
又△ABO的周长为4+ ![]() ,
,
∴△C′OD的周长为 ![]() .
.
(3)
解:连接OM,设M点的坐标为(m,n),
∵点M在抛物线上,
∴n=-m2+2m+3,
∴ ![]() ,
,
= ![]() OA·m+
OA·m+ ![]() OA′·n-
OA′·n- ![]() OA·OA′
OA·OA′
= ![]() (m+n)-
(m+n)- ![]()
= ![]() (m+n-3)
(m+n-3)
= ![]() (m2-3m)=
(m2-3m)= ![]() (m
(m ![]() )2+
)2+ ![]() .
.
∵0<m<3,∴当m= ![]() 时,n=
时,n= ![]() ,△AMA′的面积有最大值,
,△AMA′的面积有最大值,
∴当点M的坐标为( ![]() ,
, ![]() )时,△AMA′的面积有最大值,且最大值为
)时,△AMA′的面积有最大值,且最大值为 ![]() .
.
【解析】(1)需要求A′的坐标,由A(0,3)绕点O顺时针旋转90°,则A′在x轴上且OA′=OA=3,则A′(3,0);运用待定系数法求抛物线的解析式;(2)根据勾股定理易求得OB的长;由角OC′D=角OCA=角B,角C′OD=角BOA,则△C′OD~△BOA,根据相似三角形的周长比等于相似比,可先求得相似比和△BOA的周长,则可求出△OC′D的周长;(3)可设M(m,n)代入抛物线可得n与m的关系式,而 ![]() ,由面积=
,由面积= ![]() 底乘高,将上式进行化简,可得
底乘高,将上式进行化简,可得 ![]() 与m的关系式,由0<m<3,讨论m取何值时
与m的关系式,由0<m<3,讨论m取何值时 ![]() 最大.
最大.


科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x=;
(2)当点M落在AD上时,x=;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.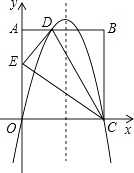
(1)求抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使四边形MENC是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2= ![]() GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2 ![]() 时,BE的长为
时,BE的长为 ![]()
![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( ) 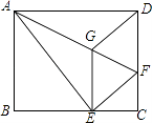
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系: ;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC= 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论错误的是( ) 
A.BD平分∠ABC
B.△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.
(1)设敬老院有x名老人,则这批牛奶共有多少盒?(用含x的代数式表示).
(2)该敬老院至少有多少名老人?最多有多少名老人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )
A.43
B.45
C.51
D.53
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com