
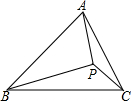
 如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.
如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心. 分析 延长CP、AP分别交AB、BC于点D、E,连接DE,利用∠PAB=∠PCB和三角形的内角和定理得出∠ADC=∠CAE,证得A、D、E、C四点共圆,得出∠EAC=∠EDC,结合∠PBC=∠PAC,证得B、E、P、D四点共圆,得出∠ADC=∠BDP=∠BEP=∠PEC=90°,证得结论成立.
解答 证明:如图,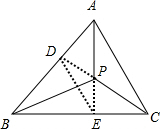
延长CP、AP分别交AB、BC于点D、E,连接DE,
∵∠PAB=∠PCB,∠APD=∠CPE,
∴∠ADC=∠AEC,
∴A、D、E、C四点共圆,
∴∠EAC=∠EDC,
又∵∠PBC=∠PAC,
∴∠PBE=∠EDP,
∴B、E、P、D四点共圆,四边形BEPD是圆内接四边形,
∴∠BDP=∠BEP=∠PEC,
∴∠ADC=∠BDP=∠BEP=∠PEC=90°,
∴CD⊥AB,AE⊥BC,
∴P为△ABC的垂心.
点评 此题考查三角形的垂心,利用垂心的定义,构造出四点共圆的条件,利用圆周角定理、平角的意义证得结论成立.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
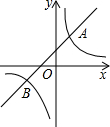 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com