Question

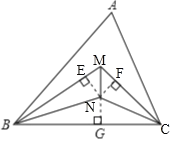
【题目】如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点，连接MN

（1）求证：MN平分∠BMC．

（2）若∠A＝60°，求∠BMN的度数．

Answer 1

【答案】（1）详见解析；（2）50°．

【解析】

（1）过点N作NG⊥BC于G，NE⊥BM于E，NF⊥CM于F，根据角平分线上的点到角的两边的距离相等可得NE=NG=NF，再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC；

（2）根据三角形内角和等于180°求出∠ABC+∠ACB，再根据角的三等分求出∠MBC+∠MCB的度数，然后利用三角形内角和定理求出∠BMC的度数，从而得解．

（1）如图，过点N作NG⊥BC于G，NE⊥BM于E，NF⊥CM于F．

∵点M、N是∠ABC与∠ACB三等分线的交点，

∴BN平分∠MBC，CN平分∠MCB．

又∵NG⊥BC，NE⊥BM，NF⊥CM，

∴NE=NG，NF=NG，

∴NE=NF，

∴MN平分∠BMC；

（2）∵MN平分∠BMC，

∴∠BMN∠BMC．

∵∠A=60°，

∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°．

∵点M、N是∠ABC与∠ACB三等分线的交点，

∴∠MBC+∠MCB（∠ABC+∠ACB）120°=80°，

∴在△BMC中，∠BMC=180°﹣（∠MBC+∠MCB）=180°﹣80°=100°，

∴∠BMN100°=50°．