
【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC,AC边上的高,连接DE,过点D作DF⊥DE交BE于点F,G为BE中点,连接AF,DG.

(1)如图1,若点F与点G重合,求证:AF⊥DF;
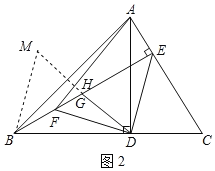
(2)如图2,请写出AF与DG之间的关系并证明.
【答案】(1)详见解析;(2)AF=2DG,且AF⊥DG,理由详见解析.
【解析】
(1)设BE交AD于点H,证出△ABD是等腰直角三角形,得出AD=BD,证明△DAE≌△DBF(ASA),得出BF=AE,DF=DE,证出△FDE是等腰直角三角形,得出∠DFE=45°,再证明△AEF是等腰直角三角形,得出∠AFE=45°,即可得出结论;
(2)延长DG至M,使GM=DG,交AF于H,连接BM,证明△BGM≌△EGD(SAS),得出∠MBE=∠FED=45°=∠EFD,BM=DE=DF,由(1)知:∠DAC=∠DBE,再证明△BDM≌△DAF(SAS),得出DM=AF=2DG,∠FAD=∠BDM,证出∠AHD=90°,即可得出结论.
(1)设BE交AD于点H,如图1所示:
∵AD,BE分别为BC,AC边上的高,
∴∠BEA=∠ADB=90°.
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD.
∵∠AHE=∠BHD,
∴∠DAC=∠DBH.
∵∠ADB=∠FDE=90°,
∴∠ADE=∠BDF.
在△DAE和△DBF中,∵ ,
,
∴△DAE≌△DBF(ASA),
∴BF=AE,DF=DE,
∴△FDE是等腰直角三角形,
∴∠DFE=45°.
∵G为BE中点,
∴BF=EF,
∴AE=EF,
∴△AEF是等腰直角三角形,
∴∠AFE=45°,
∴∠AFD=90°,
∴AF⊥DF;
(2)AF=2DG,且AF⊥DG.理由如下:
延长DG至M,使GM=DG,交AF于H,连接BM,如图2所示:
在△BGM和△EGD中,∵ ,
,
∴△BGM≌△EGD(SAS),
∴∠MBE=∠FED=45°=∠EFD,BM=DE=DF,
由(1)知:∠DAC=∠DBE,
∴∠MBD=∠MBE+∠DBE=45°+∠DBE,∠EFD=45°=∠DBE+∠BDF,
∴∠BDF=45°﹣∠DBE.
∵∠ADE=∠BDF,
∴∠ADF=90°﹣∠BDF=45°+∠DBE=∠MBD.
在△BDM和△DAF中,∵ ,
,
∴△BDM≌△DAF(SAS),
∴DM=AF=2DG,∠FAD=∠BDM.
∵∠BDM+∠MDA=90°,
∴∠MDA+∠FAD=90°,
∴∠AHD=90°,
∴AF⊥DG,
∴AF=2DG,且AF⊥DG.



科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标中,点A(1,2),将AO绕点A逆时针旋转90°,点O的对应点B恰好落在双曲线y=![]() (x>0)上,则k的值为( )
(x>0)上,则k的值为( )

A. 2 B. 3 C. 4 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,连接MN

(1)求证:MN平分∠BMC.
(2)若∠A=60°,求∠BMN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
的图象如图所示,则下列结论:①ac>0;②a-b+c<0;![]() 当
当![]() 时,
时,![]() ;
;![]() ,其中错误的结论有
,其中错误的结论有![]()
![]()
A. ②③ B. ②④ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2﹣2x﹣15,y=4x﹣23,交于A、B点(A在B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E再到达x轴上的某点F,最后运动到点B.若使点P动的总路径最短,则点P运动的总路径的长为( )
A. 10![]() B. 7
B. 7![]() C. 5
C. 5![]() D. 8
D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胖娃、猴子两人在1800米长的直线道路上跑步,胖娃、猴子两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,胖娃出发30秒后,猴子出发,猴子到终点后立即返回,并以原来的速度前进,最后与胖娃相遇,此时跑步结束. 如图,![]() (米)表示胖娃、猴子两人之间的距离,x(秒)表示胖娃出发的时间,图中折线及数据表示整个跑步过程中y与x函数关系.那么,猴子到终点后_______秒与胖娃相遇.
(米)表示胖娃、猴子两人之间的距离,x(秒)表示胖娃出发的时间,图中折线及数据表示整个跑步过程中y与x函数关系.那么,猴子到终点后_______秒与胖娃相遇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com