
分析 (1)先计算绝对值,再计算加减法;
(2)(4)根据加法交换律和结合律计算即可求解;
(3)先计算绝对值,再计算小括号里面的加减法,最后计算括号外面的乘法;
(5)(6)先计算绝对值,再从左往右计算即可求解.
解答 解:(1)|-7|-|-4|+|+2|
=7-4+2
=5;
(2)(-3.5)-(+2.5)+(-6.5)-(-12.5)
=(-3.5-6.5)+(-2.5+12.5)
=-10+10
=0;
(3)(3$\frac{1}{2}$-|-$\frac{1}{2}$|+$\frac{1}{2}$)×6
=(3$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{2}$)×6
=3$\frac{1}{2}$×6
=21;
(4)(-1$\frac{1}{4}$)-(+5$\frac{1}{4}$)-(-8$\frac{1}{2}$)-(-3$\frac{1}{2}$)
=(-1$\frac{1}{4}$-5$\frac{1}{4}$)+(8$\frac{1}{2}$+3$\frac{1}{2}$)
=-6$\frac{1}{2}$+12
=5$\frac{1}{2}$;
(5)|+2$\frac{2}{3}$|×|-9|÷|-1$\frac{1}{3}$|
=$\frac{8}{3}$×9×$\frac{3}{4}$
=18;
(6)|-$\frac{3}{4}$|÷|-1$\frac{7}{8}$|÷|-$\frac{2}{15}$|
=$\frac{3}{4}$÷1$\frac{7}{8}$÷$\frac{2}{15}$
=$\frac{3}{4}$×$\frac{8}{15}$×$\frac{15}{2}$
=3.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.


科目:初中数学 来源: 题型:解答题
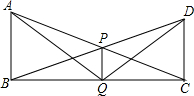 如图,AB、DC都在BC的同侧且AB⊥BC于B,DC⊥BC于C,AC,BD交于点P.PQ⊥BC于Q
如图,AB、DC都在BC的同侧且AB⊥BC于B,DC⊥BC于C,AC,BD交于点P.PQ⊥BC于Q查看答案和解析>>
科目:初中数学 来源: 题型:解答题
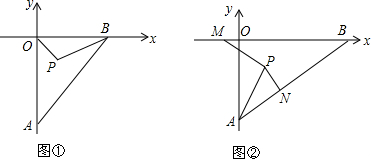
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
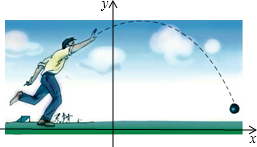 教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.
教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com