
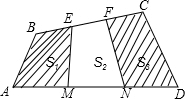
 如图所示,在四边形ABCD中,AM=MN=ND,BE=EF=FC,四边形ABEM,MEFN,NFCD的面积分别记为S1,S2和S3,则
如图所示,在四边形ABCD中,AM=MN=ND,BE=EF=FC,四边形ABEM,MEFN,NFCD的面积分别记为S1,S2和S3,则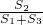 值等于________.
值等于________.
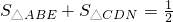 ,四边形AECN的面积=S2(2),将(1)式和(2)相加即可得出答案.
,四边形AECN的面积=S2(2),将(1)式和(2)相加即可得出答案.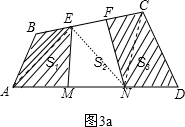 解:如图3a,连接AE、EN和NC,易知
解:如图3a,连接AE、EN和NC,易知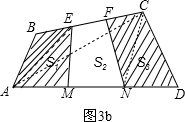
 ,
,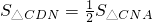
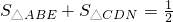
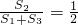 .
.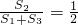 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com