
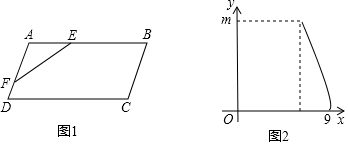
分析 (1)由题意知点E的运动路程AB+BC=9×1=9,结合AB=2BC可得答案;
(2)M为AB中点,分①当点E在AM上运动、点F在AD上运动时,即0≤x<3;②当点E在MB上运动、点F在DC上运动时,即3≤x<6;③当点E在BC上运动、点F在DC上运动时,即6≤x≤9三种情况,分别根据三角形的面积公式和割补法列式可得.
解答 解:(1)由题意知点E的运动路程AB+BC=9×1=9,
∵AB=2BC,
∴AB=6cm,BC=3cm,
故答案为:6,3;
(2)①如图1,M为AB中点,当点E在AM上运动、点F在AD上运动时,即0≤x<3,
过点F作FP⊥AB,交AB延长线于点P,
由题意知AE=AF=x,
∵四边形ABCD是平行四边形,
∴cosB=cos∠PAF=$\frac{1}{3}$,
则AP=AFcos∠PAF=$\frac{1}{3}$x,
则PF=$\sqrt{A{F}^{2}-A{P}^{2}}$=$\frac{2\sqrt{2}}{3}$x,
则y=$\frac{1}{2}$•AE•PF=$\frac{1}{2}$x•$\frac{2\sqrt{2}}{3}$x=$\frac{\sqrt{2}}{3}$x2;
②如图2,当点E在MB上运动、点F在DC上运动时,即3≤x<6,
由题意知AE=xcm,
过点F作FP⊥AB于点P,作CQ⊥AB于点Q,
∵BQ=BCcosB=3×$\frac{1}{3}$=1,
∴FP=CQ=$2\sqrt{2}$,
则y=$\frac{1}{2}$•x•2$\sqrt{2}$=$\sqrt{2}$x;
③如图③,当点E在BC上运动、点F在DC上运动时,即6≤x≤9,
由题意知,AE+BE=AD+DF=x,则BE=x-6,CE=CF=9-x,
作EP⊥AB于点P,延长PE交DF于点Q,
∵AB∥CD,
∴PQ⊥CD,∠B=∠ECQ,
∴BP=BEcosB=$\frac{1}{3}$(x-6),CQ=CEcos∠ECQ=$\frac{1}{3}$(9-x),
则PE=$\sqrt{B{E}^{2}-B{P}^{2}}$=$\frac{2\sqrt{2}}{3}$(x-6),EQ=$\frac{2\sqrt{2}}{3}$(9-x),
∴y=$\frac{1}{2}$(9-x+6)×[$\frac{2\sqrt{2}}{3}$(x-6)+$\frac{2\sqrt{2}}{3}$(9-x)]-$\frac{1}{2}$×6×$\frac{2\sqrt{2}}{3}$(x-6)-$\frac{1}{2}$×(9-x)×$\frac{1}{3}$(9-x)
=-$\frac{1}{2}$x2+(9+$\sqrt{2}$)x+3$\sqrt{2}$-$\frac{27}{2}$.
点评 本题主要考查动点问题的函数图象,根据题意弄清点E、点F运动的拐点及三角形面积的求法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=4x2+$\frac{3}{x}$-1 | B. | y=(x+4)2-x2 | C. | y=(x-2)(x+2) | D. | y=$\frac{1}{2}$(x-1)2-5x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果$\frac{a}{2}$=$\frac{b}{2}$,那么a=b | B. | 如果x=y,那么$\frac{x}{a}$=$\frac{y}{a}$ | ||
| C. | 如果mx=my,那么x=y | D. | 如果a=b,那么a+c=b-c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在直角三角形ACB中,∠C=90°,AB=4,AC=2,现操作如下:过点C作CP1⊥AB于点P1,得到Rt△CP1B,过点P1作P1P2⊥CB于点P2,得到Rt△P1P2B,按照相同的方法一直操作下去,则P1P2=$\frac{3}{2}$;PnPn+1=($\frac{\sqrt{3}}{2}$)n•$\sqrt{3}$.
在直角三角形ACB中,∠C=90°,AB=4,AC=2,现操作如下:过点C作CP1⊥AB于点P1,得到Rt△CP1B,过点P1作P1P2⊥CB于点P2,得到Rt△P1P2B,按照相同的方法一直操作下去,则P1P2=$\frac{3}{2}$;PnPn+1=($\frac{\sqrt{3}}{2}$)n•$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com