
| A. | $\frac{1}{2009}$ | B. | $\frac{1}{2008}$ | C. | -$\frac{1}{2008}$ | D. | -$\frac{1}{2009}$ |
科目:初中数学 来源: 题型:选择题
| A. | 若-a=-b,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | ||
| C. | 若ac=bc,则a=b | D. | 若(m2+1)a=(m2+1)b,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图∠ABC=90°,以AB为直径作⊙O,过C作CE切⊙O于E,CD⊥BC,AE交CD于D.
如图∠ABC=90°,以AB为直径作⊙O,过C作CE切⊙O于E,CD⊥BC,AE交CD于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
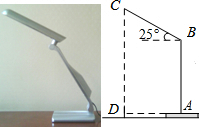 如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm.使用时发现:光线最佳时灯罩BC与水平线所成的角为25°,求光线最佳时灯罩顶端C到桌面的高度CD的长.【参考数据:sin25°=0.42,cos25°=0.91,tan25°=0.47】.
如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm.使用时发现:光线最佳时灯罩BC与水平线所成的角为25°,求光线最佳时灯罩顶端C到桌面的高度CD的长.【参考数据:sin25°=0.42,cos25°=0.91,tan25°=0.47】.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
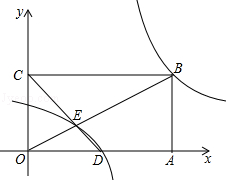 我们规定:函数y=$\frac{ax+k}{x+b}$(a、b、k是常数,k≠ab)叫广义反比例函数.当a=b=0时,广义反比例函数y=$\frac{ax+k}{x+b}$就是反比例函数y=$\frac{k}{x}$(k是常数,k≠0).
我们规定:函数y=$\frac{ax+k}{x+b}$(a、b、k是常数,k≠ab)叫广义反比例函数.当a=b=0时,广义反比例函数y=$\frac{ax+k}{x+b}$就是反比例函数y=$\frac{k}{x}$(k是常数,k≠0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com