
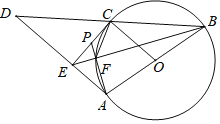
【题目】如图,AB为⊙O的直径,C为⊙O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)求证:直线EC为⊙O的切线;
(2)设BE与⊙O交于点F,AF的延长线与EC交于点P,已知∠PCF=∠CBF,PC=5,PF=3.求:cos∠PEF的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)说明OC是△BDA的中位线,利用中位线的性质,得到∠OCE=∠CED=90°,从而得到CE是圆O的切线.
(2)利用直径上的圆周角,得到△PEF是直角三角形,利用角相等,可得到△PEF∽△PEA、△PCF∽△PAC,从而得到PC=PE=5.然后求出cos∠PEF的值.
(1)证明:∵CE⊥AD于点E
∴∠DEC=90°,
∵BC=CD,
∴C是BD的中点,
又∵O是AB的中点,
∴OC是△BDA的中位线,
∴OC∥AD,
∴∠OCE=∠CED=90°,
∴OC⊥CE,
又∵点C在圆上,
∴CE是圆O的切线;
(2)连接AC,
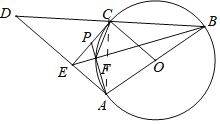
∵AB是直径,点F在圆上
∴∠AFB=∠PFE=90°=∠CEA,
∵∠EPF=∠EPA,
∴△PEF∽△PEA,
∴PE2=PF×PA,
∵∠FBC=∠PCF=∠CAF,
又∵∠CPF=∠CPA,
∴△PCF∽△PAC,
∴PC2=PF×PA,
∴PE=PC,
在直角△PEF中,
∴EF=4,cos∠PEF=![]() .
.


科目:初中数学 来源: 题型:
【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
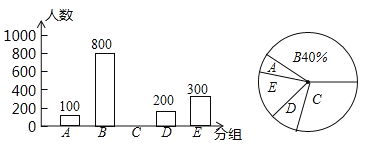
(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以BC为直径的⊙O中,点A、E为圆周上两点,过点A作AD⊥BC,垂足为D,作AF⊥CE的延长线于点F,垂足为F,连接AC、AO,已知BD=EF,BC=4.
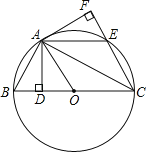
(1)求证:∠ACB=∠ACF;
(2)当∠AEF= °时,四边形AOCE是菱形;
(3)当AC= 时,四边形AOCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
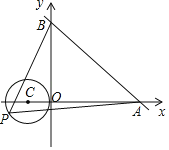
【题目】如图,直线y=﹣![]() x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
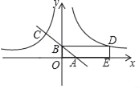
【题目】如图,一次函数y=﹣x+b交x轴于点A,交y轴于点B(0,1),与反比例函数![]() 的图象交于点C,C点的横坐标是﹣2.
的图象交于点C,C点的横坐标是﹣2.
(1)求反比例函数y1的解析式;
(2)设函数![]() 的图象与
的图象与![]() 的图象关于y轴对称,在
的图象关于y轴对称,在![]() 的图象上取一点D(D点的横坐标大于1),过D点作DE⊥x轴于点E,若四边形OBDE的面积为10,求D点的坐标.
的图象上取一点D(D点的横坐标大于1),过D点作DE⊥x轴于点E,若四边形OBDE的面积为10,求D点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com