

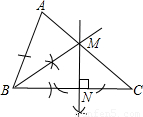
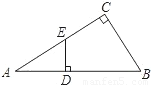
 解:(1)、(2)如图;(4分)
解:(1)、(2)如图;(4分) ∠ABC=35°,(5分)
∠ABC=35°,(5分)

 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(08)(解析版) 题型:解答题
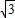 bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.
bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2009年浙江省宁波市余姚市梨洲中学质量分析数学试卷(解析版) 题型:解答题
 bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.
bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.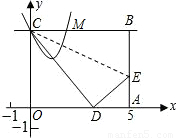
查看答案和解析>>
科目:初中数学 来源:2006年广西钦州市中考数学试卷(课标卷)(解析版) 题型:解答题
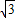 bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.
bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.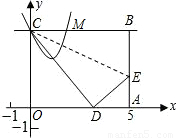
查看答案和解析>>
科目:初中数学 来源:2006年广西钦州市中考数学试卷(大纲卷)(解析版) 题型:解答题
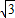 bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.
bx+c(b<0)与直线BC的另一个交点为M,问在该抛物线上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.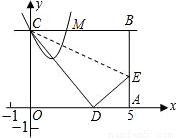
查看答案和解析>>
科目:初中数学 来源:2006年广西钦州市中考数学试卷(大纲卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com