
����Ŀ����֪����ƽ��ֱ������ϵ�У�������![]() ��
��![]() ����x����A��B���㣬��y���ڵ�C���ҶԳ���Ϊֱ��x=�D2 .
����x����A��B���㣬��y���ڵ�C���ҶԳ���Ϊֱ��x=�D2 .
��1����������ߵĽ���ʽ������D�����ꣻ
��2������P(0,t)��y���ϵ�һ�����㣬���������̽����
̽��һ����ͼ1�����PAD�����ΪS����W��t��S����0��t��4ʱ��W�Ƿ������ֵ������У����W�����ֵ�ʹ�ʱt��ֵ�����û�У�˵�����ɣ�
̽��������ͼ2���Ƿ������P��A��DΪ�������������Rt��AOC���ƣ�������ڣ����P�����ꣻ��������ڣ���˵�����ɣ�
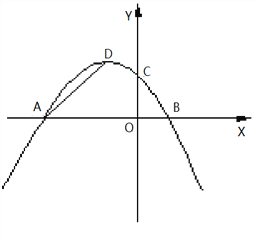
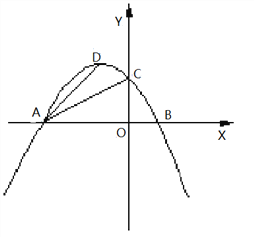
ͼ1 ͼ2
���𰸡���1��y��![]() x2x+3��D��-2��4������2������t=3ʱ��W�����ֵ��W���ֵ=18�������ڣ�ֻ����һ��P��0��2��ʹRt��ADP��Rt��AOC���ƣ�
x2x+3��D��-2��4������2������t=3ʱ��W�����ֵ��W���ֵ=18�������ڣ�ֻ����һ��P��0��2��ʹRt��ADP��Rt��AOC���ƣ�
�������������������1������������y=ax2+bx+c��a��0���Գ�����ֱ��x=![]() ������֪������
������֪������![]() ��
��![]() ���ĶԳ���Ϊֱ��x=�D2����
���ĶԳ���Ϊֱ��x=�D2����![]() ������� a��ֵ������д�������ߵĽ���ʽ�Ͷ������ꣻ��2��̽��һ����������
������� a��ֵ������д�������ߵĽ���ʽ�Ͷ������ꣻ��2��̽��һ����������![]() �Ľ���ʽ����x��y��Ľ���
�Ľ���ʽ����x��y��Ľ���![]() �����꣬��
�����꣬��![]() ����M����
����M����![]() ����
����![]() ����
����![]() ��
��![]()
![]()
![]() �ɵã�
�ɵã�![]() ����
����![]() ʱ��W�����ֵ��
ʱ��W�����ֵ��![]() ��̽�������������������������
��̽�������������������������![]() ʱ����
ʱ����![]() ����E����
����E����![]() ����
����![]() ����
����![]() ����
����![]() ������Ϊ
������Ϊ![]() �ᣬ
�ᣬ![]() �ᣬ��
�ᣬ��![]() ����
����![]() ��
��![]() ��
��![]() �����ʱ��
�����ʱ��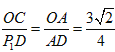 ������Ϊ
������Ϊ![]() ����
����![]() ����ʱ
����ʱ![]() ����
����![]() �����Ե�
�����Ե�![]() ʱ�����ڵ�P1��ʹ
ʱ�����ڵ�P1��ʹ![]() ����ʱP1�������Ϊ��0��2��������
����ʱP1�������Ϊ��0��2��������![]() ʱ����
ʱ����![]() ����
����![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������
������![]() ��
��![]() �����ƣ���ʱ��P2�����ڣ�����
�����ƣ���ʱ��P2�����ڣ�����![]() ʱ����ADΪֱ��������
ʱ����ADΪֱ��������![]() �İ뾶
�İ뾶![]() ��Բ��O1��y��ľ���
��Բ��O1��y��ľ���![]() ����Ϊ
����Ϊ![]() ������
������![]() ��y�����룬�����ڵ�P3��ʹ
��y�����룬�����ڵ�P3��ʹ![]() ,
,
�����ۺϿɵã�ֻ����һ��![]() ʹ
ʹ![]() ��
��![]() ���ơ�
���ơ�
���������
��1����������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��2��̽��һ����![]() ʱ��W�����ֵ��
ʱ��W�����ֵ��
��������![]() ��x����A��B���㣬��y���ڵ�C��
��x����A��B���㣬��y���ڵ�C��
��![]() ��
��
��![]() ��
��
��![]() ʱ����
ʱ����![]() ����M����ͼ��ʾ��
����M����ͼ��ʾ��
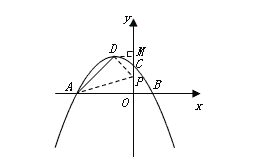
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
![]() ��
��![]()
![]()
��![]()
����![]() ʱ��W�����ֵ��
ʱ��W�����ֵ��![]() ��
��
̽���������ڣ������������
����![]() ʱ����
ʱ����![]() ����E����ͼ��ʾ��
����E����ͼ��ʾ��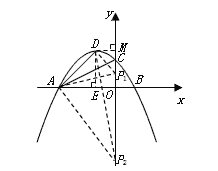
��![]() ��
��
��![]()
��![]() ��
��
��![]()
��![]() �ᣬ
�ᣬ![]() �ᣬ
�ᣬ
��![]() ��
��
��![]() ��
��
��![]()
��![]() ����
����
��ʱ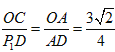 ������Ϊ
������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ʱ�����ڵ�P1��ʹ
ʱ�����ڵ�P1��ʹ![]() ����ʱP1�������Ϊ��0��2����
����ʱP1�������Ϊ��0��2����
����![]() ʱ����
ʱ����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() �����ƣ���ʱ��P2�����ڣ�
�����ƣ���ʱ��P2�����ڣ�
����![]() ʱ����ADΪֱ��������
ʱ����ADΪֱ��������![]() �İ뾶
�İ뾶![]() ��Բ��O1��y��ľ���
��Բ��O1��y��ľ���![]() ����
����![]() ��
��
��![]() ��y�����룬�����ڵ�P3��ʹ
��y�����룬�����ڵ�P3��ʹ![]() ��
��
������������ֻ����һ��![]() ʹ
ʹ![]() ��
��![]() ���ơ�
���ơ�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD����࣬�������ȱ�������ADE��DCF������AF��BE.
������д��AF��BE��������ϵ��λ�ù�ϵ�ֱ���ʲô����֤��.
������ͼ2�����������������ȱ�������ADE��DCF����Ϊ��������������ADE��DCF����EA=ED=FD=FC���ڣ�1�����еĽ����Ƿ���Ȼ����?�������жϲ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�չ��ȫ֪ʶ���������ֱ��Ǵ��һ�����5�֣�����+5�֣������һ�����2�֣�������2�֣���������20���⣬С�������15���⣬��С���÷�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˷���װ���ϰ���4500Ԫ����һ��ij��T�������������ܹ˿�ϲ�����ܿ����꣬�ϰ�����4950Ԫ�����ڶ����ÿ�ʽT�����������������һ����ͬ����ÿ�����۱ȵ�һ������9Ԫ��
��1����һ���ÿ�ʽT����ÿ�������Ƕ���Ԫ��
��2���ϰ���ÿ��120Ԫ�ļ۸����۸ÿ�ʽT���������ڶ���T�����۳� ![]() ʱ�����������������Ǿ������۴�������Ҫʹ�ڶ���������������650Ԫ��ʣ���T����ÿ���ۼ�����Ҫ����Ԫ��������=�ۼ۩����ۣ�
ʱ�����������������Ǿ������۴�������Ҫʹ�ڶ���������������650Ԫ��ʣ���T����ÿ���ۼ�����Ҫ����Ԫ��������=�ۼ۩����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����������εױߵij�Ϊ5cm��һ���ϵ����߰����ܳ��ֳɵ������ֵIJ�Ϊ1cm��������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��3a2����2a3��
��2��![]()
��3��9��x+2����x��2������3x��2��2
��4����2m+n��p����2m��n+p��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̫��Լ��15000000ǧ�ף�15000000������ÿ�ѧ���������Ա�ʾΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������100Ԫ����Ϊ+100����ô������200Ԫ����Ϊ�� ��
A.+200
B.��100
C.��200
D.��300
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com