
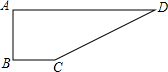
 如图,一块形如四边形的草坪,其中∠B=90°,AB=2m,BC=1m,CD=4m,AD=5m.求这块草坪的面积.
如图,一块形如四边形的草坪,其中∠B=90°,AB=2m,BC=1m,CD=4m,AD=5m.求这块草坪的面积. 分析 连接AC,作CE⊥AD于E,先根据勾股定理求出AC的长,设AE=xm,则DE=(5-x)m,由勾股定理得出方程,解方程求出AE,再根据勾股定理求出CE,这块草坪的面积=△ABC的面积+△ACD的面积,即可得出结果.
解答 解:连接AC,作CE⊥AD于E,如图所示: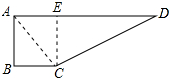
则∠AEC=∠DEC=90°,
∵∠B=90°,AB=2m,BC=1m,
∴AC=$\sqrt{{AB}^{2}+{BC}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
由勾股定理得:CE2=AC2-AE2,CE2=CD2-DE2,
∴AC2-AE2=CD2-DE2,
设AE=xm,则DE=(5-x)m,
∴5-x2=42-(5-x)2,
解得:x=$\frac{7}{5}$,
∴CE=$\sqrt{5-(\frac{7}{5})^{2}}$=$\frac{2\sqrt{19}}{5}$,
∴这块草坪的面积=△ABC的面积+△ACD的面积=$\frac{1}{2}$×1×2+$\frac{1}{2}$×5×$\frac{2\sqrt{19}}{5}$=1+$\sqrt{19}$(m2).
点评 本题考查了勾股定理、三角形面积的计算、解方程等知识;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
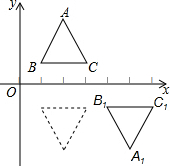 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )| A. | (5,-$\sqrt{3}$) | B. | (14,1+$\sqrt{3}$) | C. | (17,-1-$\sqrt{3}$) | D. | (20,1+$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
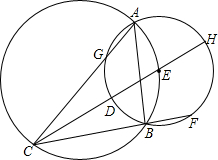 如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.
如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
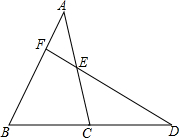 在△ABC中,点D在BC的延长线上,E是AC边中点,DE的延长线交AB于点F.
在△ABC中,点D在BC的延长线上,E是AC边中点,DE的延长线交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
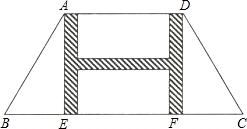 如图,有一块等腰梯形的草坪,草坪上底AD长48m,下底BC长108m,上下底之间的距离AE(或DF)是40m.现要在草坪中修建横、纵向的“H”型甬道,甬道宽度相等,设甬道的宽为x m.
如图,有一块等腰梯形的草坪,草坪上底AD长48m,下底BC长108m,上下底之间的距离AE(或DF)是40m.现要在草坪中修建横、纵向的“H”型甬道,甬道宽度相等,设甬道的宽为x m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com