
����Ŀ�����Ǹ������¶��壺��һ���ı����д����������ߵ�ƽ���͵���һ���Խ��ߵ�ƽ�����������ı���Ϊ�����ı��Σ����������ڵı߳�Ϊ����ı��εĹ��ɱ�.
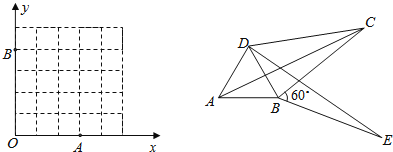
(1)д������ѧ����������ı������ǹ����ı��ε�����ͼ�ε����� �� ��
(2)��ͼ1����֪��㣨С�����εĶ��㣩O0,0��A3,0��B0,4����C Ϊͼ�����������е���һ����㣬�ı���OACB ����OA ��OB Ϊ���ɱ��ҶԽ�����ȵĹ����ı��Σ����C �����ꣻ
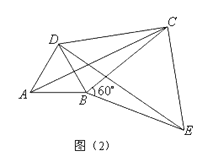
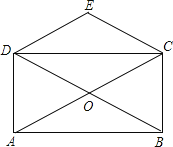
(3)��ͼ2����ABC�� BC AB ���ƶ��� B ��˳ʱ�뷽����ת60���õ�DBE ������ AD ��DC ���ı��� ABCD �ǹ����ı��Σ�����DC ��BC Ϊ���ɱߣ���DCB �Ķ���.
���𰸡���1�����Σ������Σ��𰸲�Ψһ������2��C��3,4������4,3������3����DCB=30��.
��������
��1�����ݾ����������ε����ʿɵô𰸣�
��2�����ù��ɶ����ɵ�AB=5��Ȼ���ڸ����������OC=5�ĵ㼴�ɣ�
��3������CE��������ת�����ʿɵá�ABC�ա�DBE����BC=BE����Ϊ��CBE=60����������BCE�ǵȱ������Σ���BC=CE����BCE=60�������ݹ����ı��εĶ����빴�ɶ������涨���ɵ���DCE=90������ɵ���DCB�Ķ���.
�⣺��1�����Σ������Σ��𰸲�Ψһ����
��2��![]() ��
��
��C��������ͼΪ����3,4������4,3����
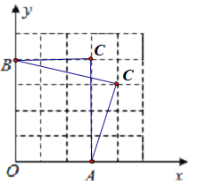
��3������CE��
����ת�����ʵã���ABC�ա�DBE����BC=BE��AC=BD��
����CBE=60����
����BCE�ǵȱ������Σ�
��BC=CE����BCE=60����
���ı���ABCDΪ�����ı��Σ�����DC��BCΪ���ɱߣ�
��![]() ��
��
��![]() ��
��
����DCE=90����
���BCD=��DCE����BCE=90����60��=30��.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��60��A��Ʒ��30��B��Ʒ������1080Ԫ������50��A��Ʒ��20��B��Ʒ������880Ԫ��
��1��A��B������Ʒ�ĵ��۷ֱ��Ƕ���Ԫ��
��2����֪���̵깺��B��Ʒ�ļ����ȹ���A��Ʒ�ļ�����2����4���������Ҫ����A��B������Ʒ���ܼ���������32�����Ҹ��̵깺���A��B������Ʒ���ܷ��ò�����296Ԫ����ô���̵����ļ��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ĩ������ȥͼ��ݽ��飬��ͼ������ҵľ��� y ��ǧ�ף���ʱ�� x �����ӣ��ĺ���ͼ����ͼ����Ϣ������������⣺
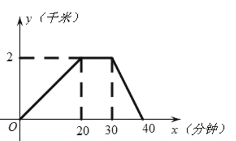
��1����������ͼ����ж�Զ��
��2��������ͼ���ͣ���˶ʱ�䣿
��3��������ͼ��ݷ��ؼ������˶���ʱ�䣿
��4������ȫ�̵�ƽ���ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ��7����B��ʾ����Ϊ5����C����A����B�ľ�����ȣ�����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����������������˶������˶���ʱ��Ϊt��t��0���룮
��1����C��ʾ�������� ����
��2����t���ڶ�����ʱ����P�����B����
��3����P��ʾ�������� �����ú���t�Ĵ���ʽ��ʾ����
��4����t���ڶ�����ʱ��PC֮��ľ���Ϊ2����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ������ ��
A����������״����С���ʵ���ȫһ����5�������1��������������һ����һ���Ǻ���
B������Ԥ�������콵ˮ����10%������ָ������10%��ʱ�������
C��ij�ط���һ�ָ�����Ʊ���н�����ǧ��֮һ����ô�������ֲ�Ʊ1000�ţ�һ�����н�
D��������һö����Ӳ�ң���5�ζ������泯�ϣ����������Ȼ�������泯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˾���˭����ý��е�һ�ſ��ձ����볡ȯ��������������µ�һ����Ϸ��
�ڴ����б�ŷֱ�Ϊ1��2��3�ĺ��������ͱ��Ϊ4�İ���һ�����ĸ��������ɫ���Ų�ͬ�⣬û���κα����������֮ǰ��С����ȣ�������˶������۾����ȼ������Σ�ÿ������һ���Ѽ�������������Żؿڴ�������������ֻ��һ����������������������Ǻ�ɫ����1�֣�����0�֣���������������ǰ�ɫ���ҵ�1�֣������ҵ�0�� ���÷ָߵĻ���볡ȯ������÷���ͬ����Ϸ������
��1�������б�����״ͼ���1�ֵĸ��ʣ�
��2�������Ϸ�Ƿ�ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1��A��E��F��C��ͬһֱ���ϣ�AE=CF����E��F�ֱ���DE��AC��BF��AC��AB=CD��G��EF���е�����֤����Ľ��ۡ����� �SABC�ı�EC��AC�����ƶ���Ϊͼ��2��ʱ�������������䣬�������ۻ�������Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ԡ���ɫ����,��������Ϊ�����2019���й����������ղ�����(��Ʊ�������)�������Ļ,����������Ȼ�������ľ��ʹ���,������̶�����������300�����ҹ��̶�����������400������ʱ�����,�ҹ��̶�ÿ��ȼ��̶Ӷ�����10��������,����̶�ÿ�����������Ͷ��ٸ���
����ͬѧ���еķ�������:
![]()
����������Ϣ,�����������:
��1��С��ͬѧ���з����е�x��ʾ ��С��ͬѧ���з����е�y�� ��
��2��������ѡ��ķ��̣�������̶�ÿ�����������Ͷ��ٸ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��CE��BD��DE��AC��
��1��֤�����ı���OCEDΪ���Σ�
��2����AC=4�����ı���CODE���ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com