

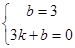 ,
,
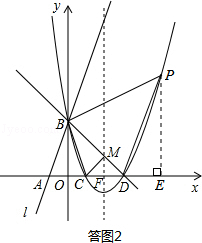
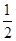 (3+n)•m﹣
(3+n)•m﹣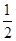 ×3×3﹣
×3×3﹣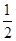 (m﹣3)•n=6,
(m﹣3)•n=6,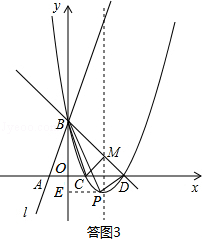
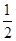 (3+m)•(﹣n)+
(3+m)•(﹣n)+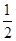 ×3×3﹣
×3×3﹣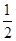 (3﹣n)•m=6,
(3﹣n)•m=6,

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
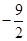 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为( ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成 ,最小值为2”.你认为( )
,最小值为2”.你认为( )| A.甲对 | B.乙对 | C.甲、乙都对 | D.甲乙都不对 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(-3,0) | B.(-2,0) |
| C.x=-3 | D.x=-2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
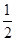 x2-7x+
x2-7x+ ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )| A.y1>y2>y3 | B.y1<y2<y3 |
| C.y2>y3>y1 | D.y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.ac>0 |
| B.方程ax2+bx+c=0的两根是x1=-1,x2=3 |
| C.2a-b=0 |
| D.当y>0时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
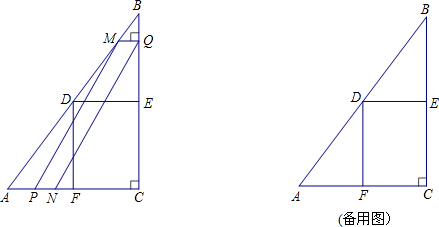
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com