
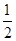 ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;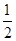 ∠BAD, (1)中的结论是否仍然成立?不用证明.
∠BAD, (1)中的结论是否仍然成立?不用证明. 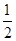 ∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.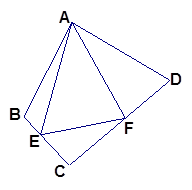

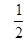 ∠BAD.
∠BAD.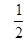 ∠BAD.
∠BAD.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
 和等腰
和等腰 中,
中, ,
, ,
, ,点
,点 、
、 、
、 、
、 在一条直线上。当点
在一条直线上。当点 和点
和点 重合时,等腰
重合时,等腰 静止不动,等腰
静止不动,等腰 从
从 出发,沿线段
出发,沿线段 方向以每秒1个单位长度的速度匀速运动,当
方向以每秒1个单位长度的速度匀速运动,当 点与
点与 点重合时,停止运动。设运动时间为
点重合时,停止运动。设运动时间为 秒
秒 。
。

 、12、14秒时,
、12、14秒时, 的长度分别为 、 、 ;
的长度分别为 、 、 ; 的运动过程中,设等腰
的运动过程中,设等腰 和等腰
和等腰 重叠部分的面积为
重叠部分的面积为 ,请直接写出
,请直接写出 与
与 的函数关系式和相应的自变量
的函数关系式和相应的自变量 的取值范围;
的取值范围; 点与
点与 点重合时,将等腰
点重合时,将等腰 绕点
绕点 顺时针转
顺时针转 角(
角( ),连接
),连接 、
、 ,过点
,过点 作
作 ,延长
,延长 。
。 ;
; ,求
,求 的长度。
的长度。查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010-2011学年山东省德州七年级第一学期期末数学试卷 题型:解答题
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC;OE平分∠BOC.
【小题1】写出图中∠BOD与∠AOE的补角;
【小题2】如果∠COD=25°,那么∠COE=_______;如果∠COD=60°,那么∠COE=________;
【小题3】试猜想∠COD与∠COE具有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届北京昌平区中考模拟数学题卷 题型:解答题
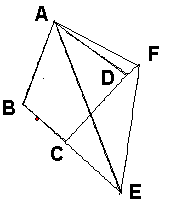
【小题1】如图25-1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF= ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;
【小题2】如图25-2在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF= ∠BAD, (1)中的结论是否仍然成立?不用证明.
∠BAD, (1)中的结论是否仍然成立?不用证明.
【小题3】如图25-3在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF= ∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com