
分析 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD和BC的关系,根据三角形ABC的面积,即可解题.
解答 解:等边三角形三线合一,即D为BC的中点,
∴设BD=DC=a,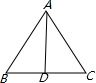
在Rt△ABD中,AB=2a,BD=a,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{(2a)^{2}-{a}^{2}}=\sqrt{3}a$,
∴△ABC的面积为$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2a×$\sqrt{3}$a=16$\sqrt{3}$cm2,
解得:a=4cm,
故答案为:4.
点评 本题考查了勾股定理在直角三角形中的运用,等边三角形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2是8的立方根 | B. | ±4是64的立方根 | ||
| C. | -$\frac{1}{3}$是-$\frac{1}{27}$的立方根 | D. | (-4)3的立方根是-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 客车 | 座位 | 售价(万元) | 每座日租金(元) | 出租率 |
| 大型 | 40 | 45 | 80 | 55% |
| 中型 | 25 | 35 | 80 | 70% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
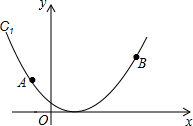 如图,在平面直角坐标系中,过点A(-2,2),点B(4,4)的抛物线C1的函数表达式y=ax2+bx.求抛物线C1的函数表达式及其对称轴.
如图,在平面直角坐标系中,过点A(-2,2),点B(4,4)的抛物线C1的函数表达式y=ax2+bx.求抛物线C1的函数表达式及其对称轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com