
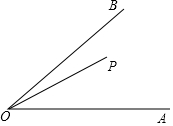
 如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$. 分析 根据轴对称图形的性质,作出P关于OA、OB的对称点M、N,连接AB,根据两点之间线段最短得到最小值线段,再构造直角三角形,利用勾股定理求出MN的值即可.
解答 解:分别作P关于OA、OB的对称点M、N.
连接MN交OA、OB交于Q、R,则△PQR符合条件.
连接OM、ON,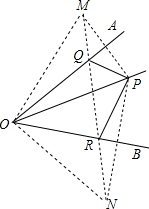
则OM=ON=OP=10,
∠MON=∠MOP+∠NOP=2∠AOB=2×45°=90°,
故△MON为等腰直角三角形.
∴MN=$\sqrt{1{0}^{2}+1{0}^{2}}=10\sqrt{2}$,
所以△PQR周长的最小值为10$\sqrt{2}$,
故答案为:$10\sqrt{2}$
点评 此题考查了轴对称最短路径问题,根据题意构造出对称点,转化为直角三角形的问题是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
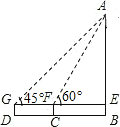 如图,初三年级某同学要测量校园内的旗杆AB的高度.在地面上C点用测角仪测得旗杆顶A点的仰角为∠AFE=60°,再沿着直线BC后退8米到D,在D点又测得旗杆顶A的仰角∠AGE=45°.已知测角仪DG的高度为1.6米,求旗杆AB的高度.($\sqrt{3}$的近似值取1.7,结果保留1位小数)
如图,初三年级某同学要测量校园内的旗杆AB的高度.在地面上C点用测角仪测得旗杆顶A点的仰角为∠AFE=60°,再沿着直线BC后退8米到D,在D点又测得旗杆顶A的仰角∠AGE=45°.已知测角仪DG的高度为1.6米,求旗杆AB的高度.($\sqrt{3}$的近似值取1.7,结果保留1位小数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,观察图象,判断下列说法错误的是( )
如图,观察图象,判断下列说法错误的是( )| A. | 方程组$\left\{\begin{array}{l}y=2x-1\\ y=-\frac{3}{5}x+\frac{8}{5}\end{array}\right.$.的解是 $\left\{\begin{array}{l}x=1\\ y=1.\end{array}\right.$ | |
| B. | 不等式-$\frac{3}{5}$x+$\frac{8}{5}$≤2x-1的解集是x≥1 | |
| C. | 不等式-$\frac{3}{5}$x+$\frac{8}{5}$>2x-1的解集是x>1 | |
| D. | 方程-$\frac{3}{5}$x+$\frac{8}{5}$=2x-1的解是x=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,AC=8,点D在AB边上,且AD=BD=CD=5,在△ABC外,作等边△ACE.
已知:如图,△ABC中,AC=8,点D在AB边上,且AD=BD=CD=5,在△ABC外,作等边△ACE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1$\frac{1}{2}$(a+b) | B. | a+1$\frac{1}{2}$+b | C. | 1$\frac{1}{2}$a+b | D. | $\frac{3}{2}$a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com