
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根据内心的概念证明△POC∽△QBC,根据相似三角形的性质得到$\frac{PC}{CQ}$=$\frac{OB}{OA}$,证明△PCQ∽△AOB,得到∠CPQ=∠A=15°,证明△COQ≌△MOQ即可.
解答 解:∵∠AOB=90°,∠ACO=90°,
∴∠AOC=∠ABO,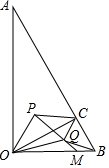 ∵P,Q分别为△AOC和△BOC的内心,
∵P,Q分别为△AOC和△BOC的内心,
∴∠POC=∠QBC,∠PCO=∠BCQ=45°,
∴△POC∽△QBC,
∴$\frac{PC}{CQ}$=$\frac{OC}{BC}$,
∵$\frac{OB}{OA}$=$\frac{OC}{BC}$,
∴$\frac{PC}{CQ}$=$\frac{OB}{OA}$,又∠AOB=∠PCQ=90°,
∴△PCQ∽△AOB,
∴∠CPQ=∠A=15°,
由内心的概念可知,∠OPC=90°+$\frac{1}{2}$×15°,
∴∠OPM=90°+$\frac{1}{2}$×15°-15°,
∵∠POM=90°-$\frac{1}{2}$∠AOC=90°-$\frac{1}{2}$×75°,
∴∠PMO=45°,
在△COQ和△MOQ中,
$\left\{\begin{array}{l}{∠COQ=∠MOQ}\\{∠OCQ=∠OMQ}\\{OQ=OQ}\end{array}\right.$,
∴△COQ≌△MOQ,
∴OM=OC=1,
故选:B.
点评 本题考查的是三角形的内接圆和内心的概念、相似三角形的判定和性质、全等三角形的判定和性质,掌握三角形的内接圆和内心的概念是解题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
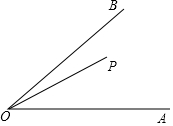 如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
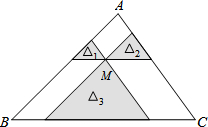 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com