等腰三角形底边长为6cm,腰长为5cm,则该三角形的面积等于________,它腰上的高等于________.
12

分析:根据勾股定理求出AD的长,然后即可求出该三角形的面积,再根据该三角形的面积还等于

AC•BE,即可求出它腰上的高.
解答:
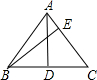
解:如图所示:AD⊥BC,BE为腰上的高,AB=AC=5.BC=6.
∵△ABC为等腰三角形,AD⊥BC,
∴BD=CD=

BC=3,
∴AD=

=

=4,
∴该三角形的面积等于

AD•BC=

×4×6=12;
∵该三角形的面积还等于

AC•BE,
∴

AC•BE=12,
∴BE=

.
故答案为:12;

.
点评:此题主要考查勾股定理,等腰三角形的性质等知识点,此题的关键是知道三角形的面积

AC•BE=

AD•BC.

 名校课堂系列答案
名校课堂系列答案