
【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( ) 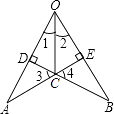
A.2对
B.3对
C.4对
D.5对
【答案】C
【解析】解:①△ODC≌△OEC
∵BD⊥AO于点D,AE⊥OB于点E,OC平分∠AOB
∴∠ODC=∠OEC=90°,∠1=∠2
∵OC=OC
∴△ODC≌△OEC(AAS)
∴OE=OD,CD=CE;
②△ADC≌△BEC
∵∠CDA=∠CEB=90°,∠3=∠4,CD=CE
∴△OBE≌△OCD(AAS)
∴AC=BC,AD=BE,∠B=∠A;
③△OAC≌△OBC
∵OD=OE
∴OA=OB
∵OA=OB,OC=OC,AC=BC
∴△ABO≌△ACO(SSS);
④△OAE≌△OBD
∵∠ODB=∠OEA=90°,OA=OB,OD=OE
∴△AEC≌△ADB(HL).
故选C.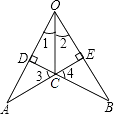
根据已知条件可以找出题目中有哪些相等的角以及线段,然后猜想可能全等的三角形,然后一一进行验证,做题时要由易到难,循序渐进.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 三角形分为等边三角形和三边不相等的三角形
B. 等边三角形不是等腰三角形
C. 等腰三角形是等边三角形
D. 三角形分为锐角三角形,直角三角形,钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
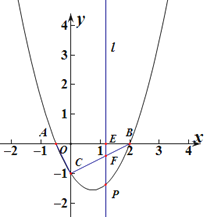
【题目】如图,二次函数 ![]() 的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
(1)求二次函数解析式;
(2)直线![]() 与
与![]() 轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
①求线段PF取得最大值时,OE的长;
②四边形ACPB的面积是否存在最大值?如果存在求出此最大值和点P的坐标;如果不存在,说明理由.
(3)不解方程组,直接写出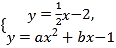 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
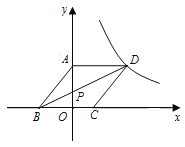
【题目】如图,边长为![]() 的菱形ABCD的顶点D在反比例函数
的菱形ABCD的顶点D在反比例函数![]() (
(![]() >0)的图象上,A点的坐标为(0,4),连接BD,交
>0)的图象上,A点的坐标为(0,4),连接BD,交![]() 轴于点P.
轴于点P.
(1)求菱形边长![]() 及点C坐标;
及点C坐标;
(2)![]() 沿着线段BD平移,当点C落在
沿着线段BD平移,当点C落在![]() (
(![]() >0)上时,求点B沿BD方向移动的距离.
>0)上时,求点B沿BD方向移动的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论正确的有____________.(只填序号)
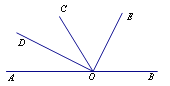
①∠AOD与∠BOE互为余角;
②OD平分∠COA;
③∠BOE=56°40′,则∠COE=61°40′;
④∠BOE=2∠COD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com