Question

【题目】如图，折叠矩形的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EC的长．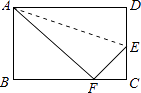

Answer 1

【答案】解：∵四边形ABCD为矩形， ∴DC=AB=8，AD=BC=10，∠B=∠D=∠C=90°，
∵折叠矩形的一边AD，使点D落在BC边的点F处
∴AF=AD=10，DE=EF，
在Rt△ABF中，BF= = =6，
∴FC=BC﹣BF=4，
设EC=x，则DE=8﹣x，EF=8﹣x，
在Rt△EFC中，
∵EC2+FC2=EF2 ，
∴x2+42=（8﹣x）2 ， 解得x=3，
∴EC的长为3cm
【解析】根据矩形的性质得DC=AB=8，AD=BC=10，∠B=∠D=∠C=90°，再根据折叠的性质得AF=AD=10，DE=EF，在Rt△ABF中，利用勾股定理计算出BF=6，则FC=4，设EC=x，则DE=EF=8﹣x，在Rt△EFC中，根据勾股定理得x2+42=（8﹣x）2 ， 然后解方程即可．