
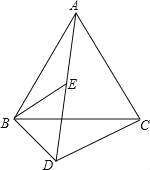
【题目】如图,已知△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA﹣DB=DC.
【答案】证明见解析.
【解析】试题分析:根据等边三角形的性质,可得AB与BC的关系,BD、BE、DE的关系,根据三角形全等的判定,可得△ABE与△CBD的关系,根据全等三角形的性质,可得对应边相等,根据线段的和差,等量代换,可得证明结果.
试题解析:
△ABC和△BDE都是等边三角形
∴AB=BC,BE=BD=DE(等边三角形的边相等),
∠ABC=∠EBD=60°(等边三角形的角是60°).
∴∠ABC﹣∠EBC=∠EBD﹣∠EBC
∠ABE=CBD (等式的性质),
在△ABE和△CBD中,
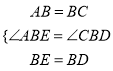 ,
,
∴△ABE≌△CBD(SAS)
∴AE=DC(全等三角形的对应边相等).
∵AD﹣DE=AE(线段的和差)
∴AD﹣BD=DC(等量代换).


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将一幅三角板按照如图所示的位置放置在直线![]() 上,
上, ![]() =
=![]() =45°,
=45°,![]() =
=![]() =90°,
=90°,![]() =30°,
=30°,![]() =60°.将含45°锐角的三角板
=60°.将含45°锐角的三角板![]() 固定不动,含30°锐角的三角板
固定不动,含30°锐角的三角板![]() 绕点
绕点![]() 顺时针旋转1周,在此过程中:
顺时针旋转1周,在此过程中:
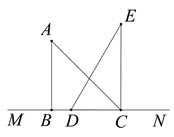
(1)如图,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() .
.
①若![]() 平分
平分![]() ,试问
,试问![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
②若![]() ,
, ![]() ,
, ![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 这三者之间有什么数量关系?请用一个含
这三者之间有什么数量关系?请用一个含![]() 、
、![]() 、
、![]() 的等式来表达,并说明理由.
的等式来表达,并说明理由.
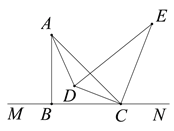
(2)如图, ![]() 是
是![]() 的角平分线,当
的角平分线,当![]() 所在直线与
所在直线与![]() 所在直线互相垂直时,请直接写出
所在直线互相垂直时,请直接写出![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多项式﹣x+x3+1﹣x2按x的升幂排列正确的是( )
A.x2﹣x+x3+1
B.1﹣x2+x+x3
C.1﹣x﹣x2+x3
D.x3﹣x2+1﹣x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,﹣1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同,甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)求甲、乙每天各加工零件多少个?
(2)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com