
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求点P与点P′之间的距离;
(2)求∠APB的度数.
【答案】
(1)解:连接PP′,由题意可知BP′=PC=10,AP′=AP,
∠PAC=∠P′AB,而∠PAC+∠BAP=60°,
所以∠PAP′=60度.故△APP′为等边三角形,
所以PP′=AP=AP′=6

(2)解:利用勾股定理的逆定理可知:
PP′2+BP2=BP′2,所以△BPP′为直角三角形,且∠BPP′=90°
可求∠APB=90°+60°=150°
【解析】(1)由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′;(2)由△APP′为等边三角形,得∠APP′=60°,在△PP′B中,已知三边,用勾股定理逆定理证出直角三角形,得出∠P′PB=90°,可求∠APB的度数.
【考点精析】本题主要考查了勾股定理的逆定理和旋转的性质的相关知识点,需要掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.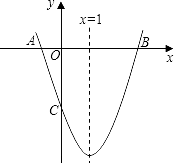
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣3,0),与反比例函数y= ![]() 在第一象限的图象交于点B(3,m),连接BO,若△AOB面积为9,
在第一象限的图象交于点B(3,m),连接BO,若△AOB面积为9, 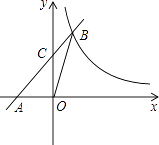
(1)求反比例函数的表达式和直线AB的表达式;
(2)若直线AB与y轴交于点C,求△COB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( ) 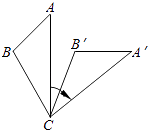
A.110°
B.80°
C.40°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.将点A、B、C的横坐标不变,纵坐标都乘以-1,分别得到点A1、B1、C1
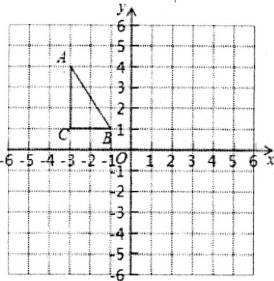
(1)写出△A1B1C1,三个顶点的坐标________;
(2)在图中画出△A1B1C1,则△ABC与△A1B1C1关于________对称;
(3)若以点A、C、P为顶点的三角形与△ABC全等,直接写出所有符合条件的点P的坐标________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系: 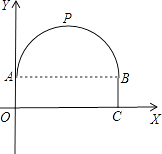
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形纸片 ABC 中,AB=15cm,AC=9cm,BC=12cm, 现将边 AC 沿过点 A 的直线折叠,使它落在 AB 边上.若折痕交 BC 于点 D,点 C 落在点 E 处,你能求出 BD 的长吗?请写出求解过程.
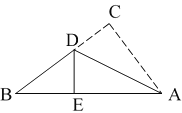
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F. 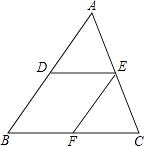
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com