
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系: 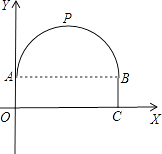
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
科目:初中数学 来源: 题型:
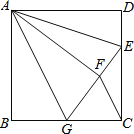
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,则下列结论:①
,则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() 与
与![]() 的面积相等;⑤
的面积相等;⑤![]() ,其中正确的个数是( )
,其中正确的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求点P与点P′之间的距离;
(2)求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图,若点D为线段AC的中点,求证:AD=CE;

(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
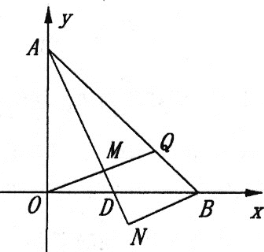
【题目】在平面直角坐标系xOy中,直线AB交y轴于A点,交X轴于B点,A(0,6),B(6,0).点D是线段BO上一点,BN⊥AD交AD的延长线于点N.
(1)如图,若OM∥BN交AD于点M.点O作0G⊥BN,交BN的延长线于点G,求证:AM=BG

(2)如图,若∠ADO=67.5°,OM∥BN交AD于点M,交AB于点Q,求![]() 的值.
的值.
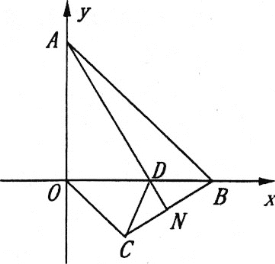
(3)如图,若OC∥AB交BN的延长线于点C.请证明:∠CDN+2∠BDN=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.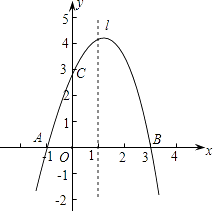
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
(4)若抛物线顶点为D,点Q为直线AC上一动点,当△DOQ的周长最小时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
![]() 在图中画出与
在图中画出与![]() 关于直线l成轴对称的
关于直线l成轴对称的![]() ;
;
![]() 三角形ABC的面积为______;
三角形ABC的面积为______;
![]() 以AC为边作与
以AC为边作与![]() 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与![]() 全等;
全等;
![]() 在直线l上找一点P,使
在直线l上找一点P,使![]() 的长最短.
的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
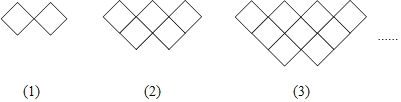
【题目】如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(n)个图形中面积为1的正方形的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com