
 x2+bx(b为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
x2+bx(b为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
 x2+bx过点D(40,8)可得8=
x2+bx过点D(40,8)可得8= ×402+40•b,
×402+40•b, x2-0.2x=
x2-0.2x= x2-
x2- x=
x= (x-10)2-1,其顶点坐标为(10,-1),
(x-10)2-1,其顶点坐标为(10,-1),

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
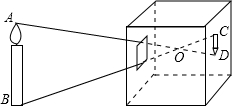 如图所示的小孔成像问题中,光线穿过小孔,在竖直的屏幕上形成倒立的实像.若像的长度CD=2cm,点O到AB的距离是12cm,到CD的距离是3cm.则蜡烛的高度AB为
如图所示的小孔成像问题中,光线穿过小孔,在竖直的屏幕上形成倒立的实像.若像的长度CD=2cm,点O到AB的距离是12cm,到CD的距离是3cm.则蜡烛的高度AB为查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 汪老师要装修自己带阁楼的新居(如图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是
汪老师要装修自己带阁楼的新居(如图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com