
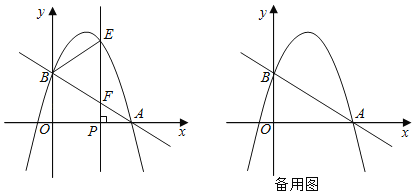
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() ЗжБ№НЛxжсЃЌyжсгкЕуAЃЌBЃЌХзЮяЯпyЃНЉx2+bx+cОЙ§ЕуAЃЌBЃЌЕуPЪЧxжсЩЯвЛИіЖЏЕуЃЌЙ§ЕуPзїДЙжБгкxжсЕФжБЯпЗжБ№НЛХзЮяЯпКЭжБЯпABгкЕуEКЭЕуF.ЩшЕуPЕФКсзјБъЮЊm.
ЗжБ№НЛxжсЃЌyжсгкЕуAЃЌBЃЌХзЮяЯпyЃНЉx2+bx+cОЙ§ЕуAЃЌBЃЌЕуPЪЧxжсЩЯвЛИіЖЏЕуЃЌЙ§ЕуPзїДЙжБгкxжсЕФжБЯпЗжБ№НЛХзЮяЯпКЭжБЯпABгкЕуEКЭЕуF.ЩшЕуPЕФКсзјБъЮЊm.
(1)ЧѓетЬѕХзЮяЯпЫљЖдгІЕФКЏЪ§БэДяЪН.
(2)ЕуPдкЯпЖЮOAЩЯЪБЃЌШєвдBЁЂEЁЂFЮЊЖЅЕуЕФШ§НЧаЮгыЁїFPAЯрЫЦЃЌЧѓmЕФжЕЃЛ
(3)ШєEЁЂFЁЂPШ§ИіЕужаЧЁгавЛЕуЪЧЦфЫќСНЕуЫљСЌЯпЖЮЕФжаЕу(Ш§ЕужиКЯГ§Эт)ЃЌГЦEЁЂFЁЂPШ§ЕуЮЊЁАЙВжюЕуЁБ.жБНгаДГіEЁЂFЁЂPШ§ЕуГЩЮЊЁАЙВжюЕуЁБЪБmЕФжЕ.
ЁОД№АИЁП(1)yЃНЉx2+![]() x+2ЃЛ(2)mЃН
x+2ЃЛ(2)mЃН![]() Лђ
Лђ![]() ЃЛ(3) -1Лђ-
ЃЛ(3) -1Лђ-![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉ![]() НЛxжсЃЌyжсгкЕуAЃЌBЃЌЧѓГіЕуAЁЂBЕФзјБъЃЌПЩЕУcЃН2ЃЌдђХзЮяЯпБэДяЪНЮЊЃКyЃНЉx2+bx+2ЃЌНЋЕуAЕФзјБъДњШыЩЯЪНЃЌМДПЩЧѓНтЃЛ
НЛxжсЃЌyжсгкЕуAЃЌBЃЌЧѓГіЕуAЁЂBЕФзјБъЃЌПЩЕУcЃН2ЃЌдђХзЮяЯпБэДяЪНЮЊЃКyЃНЉx2+bx+2ЃЌНЋЕуAЕФзјБъДњШыЩЯЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйЕБЁЯEBFЮЊжБНЧЪБЃЌдђtanЁЯBEFЃН![]() ЃЌдђBE2ЃН4BF2ЃЌИљОнЙДЙЩЖЈРэСаЗНГЬЧѓНтМДПЩЃЛЂкЕБЁЯBEFЮЊжБНЧЪБЃЌдђEFЃН
ЃЌдђBE2ЃН4BF2ЃЌИљОнЙДЙЩЖЈРэСаЗНГЬЧѓНтМДПЩЃЛЂкЕБЁЯBEFЮЊжБНЧЪБЃЌдђEFЃН![]() BEЃЌгыЂйЭЌРэМДПЩЧѓНтЃЛ
BEЃЌгыЂйЭЌРэМДПЩЧѓНтЃЛ
ЃЈ3ЃЉгУmПЩБэЪОГіPЁЂFЁЂEЕФзјБъЃЌгЩЬтвтПЩжЊгаFЮЊЯпЖЮPEЕФжаЕуЁЂPЮЊЯпЖЮEFЕФжаЕуЛђEЮЊЯпЖЮPFЕФжаЕуЃЌПЩЗжБ№ЕУЕНЙигкmЕФЗНГЬЃЌПЩЧѓЕУmЕФжЕЃЎ
НтЃКЃЈ1ЃЉАбx=0ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() =2.
=2.
Абy=0ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЁрx=4.
ЃЌЁрx=4.
ЁрЕуAЁЂBЕФзјБъЗжБ№ЮЊ(4ЃЌ0)ЁЂ(0ЃЌ2)ЃЌ
ЁрcЃН2ЃЌ
ЁрХзЮяЯпБэДяЪНЮЊЃКyЃНЉx2+bx+2ЃЌ
НЋЕуAЕФзјБъДњШыЩЯЪНЕУЃЌ
0ЃНЉ16+4b+2ЃЌ
ЁрbЃН![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉx2+![]() x+2ЃЛ
x+2ЃЛ
ЃЈ2ЃЉtanЁЯOABЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЕуPЕФКсзјБъЮЊmЃЌдђЕуEЁЂFЕФзјБъЗжБ№ЮЊЃК(mЃЌЉm2+![]() m+2)ЁЂ(mЃЌЉ
m+2)ЁЂ(mЃЌЉ![]() m+2)ЃЌ
m+2)ЃЌ
ЂйЕБЁЯEBFЮЊжБНЧЪБЃЌ
вдBЁЂEЁЂFЮЊЖЅЕуЕФШ§НЧаЮгыЁїFPAЯрЫЦЃЌдђЁЯBEFЃНЁЯOABЃЌ
дђtanЁЯBEFЃН![]() ЃЌдђBE2ЃН4BF2ЃЌ
ЃЌдђBE2ЃН4BF2ЃЌ
МДЃКm2+(Љm2+![]() m+2
m+2![]() mЉ2)2ЃН4[m2+(Љ
mЉ2)2ЃН4[m2+(Љ![]() m+2Љ2)2]ЃЌ
m+2Љ2)2]ЃЌ
НтЕУЃКmЃН![]() Лђ
Лђ![]() (ЩсШЅ
(ЩсШЅ![]() )ЃЛ
)ЃЛ
ЂкЕБЁЯBEFЮЊжБНЧЪБЃЌ
дђEFЃН![]() BEЃЌ
BEЃЌ
ЁрЉm2+![]() m+2
m+2![]() mЉ2=
mЉ2=![]() mЃЌ
mЃЌ
НтЕУ
m1=![]() ЃЌm2=0ЃЈЩсШЅЃЉ.
ЃЌm2=0ЃЈЩсШЅЃЉ.
злЩЯЃЌmЃН![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕуPЕФКсзјБъЮЊmЃЌдђЕуPЁЂEЁЂFЕФзјБъЗжБ№ЮЊЃК(mЃЌ0)ЁЂ(mЃЌЉm2+![]() m+2)ЁЂ(mЃЌЉ
m+2)ЁЂ(mЃЌЉ![]() m+2)ЃЌ
m+2)ЃЌ
ЁпEЁЂFЁЂPШ§ЕуЮЊЁАЙВаГЕуЁБЃЌ
ЁргаFЮЊЯпЖЮPEЕФжаЕуЁЂPЮЊЯпЖЮFEЕФжаЕуЛђEЮЊЯпЖЮPFЕФжаЕуЃЌ
ЕБFЮЊЯпЖЮPEЕФжаЕуЪБЃЌдђга2ЃЈ-![]() m+2ЃЉ=-m2+
m+2ЃЉ=-m2+![]() m+2ЃЌНтЕУm=4ЃЈШ§ЕужиКЯЃЌЩсШЅЃЉЛђm=
m+2ЃЌНтЕУm=4ЃЈШ§ЕужиКЯЃЌЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
ЕБPЮЊЯпЖЮFEЕФжаЕуЪБЃЌдђга-![]() m+2+ЃЈ-m2+
m+2+ЃЈ-m2+![]() m+2ЃЉ=0ЃЌНтЕУm=4ЃЈЩсШЅЃЉЛђm=-1ЃЛ
m+2ЃЉ=0ЃЌНтЕУm=4ЃЈЩсШЅЃЉЛђm=-1ЃЛ
ЕБEЮЊЯпЖЮFPЕФжаЕуЪБЃЌдђга-![]() m+2=2ЃЈ-m2+
m+2=2ЃЈ-m2+![]() m+2ЃЉЃЌНтЕУm=4ЃЈЩсШЅЃЉЛђm=-
m+2ЃЉЃЌНтЕУm=4ЃЈЩсШЅЃЉЛђm=-![]() ЃЛ
ЃЛ
злЩЯПЩжЊЕБEЁЂFЁЂPШ§ЕуГЩЮЊЁАЙВаГЕуЁБЪБmЕФжЕЮЊ-1Лђ-![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDжаЃЌABЃНACЃЌЕуEЁЂFЗжБ№ЮЊБпABЁЂBCЩЯЕФЕуЧвAEЃНBFЃЌСЌНгCEЁЂAFНЛгкЕуHЃЌСЌНгDHНЛAGгкЕуOЃЌдђЯТСаНсТлЂйЁїABFЁеЁїCAEЃЛЂкЁЯAHCЃН120ЁуЃЛЂлAE+CHЃОCDЃЌжае§ШЗЕФЪЧ____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌEЪЧБпACЩЯШЮвтвЛЕуЃЈЕуEгыЕуAЃЌCВЛжиКЯЃЉЃЌвдCEЮЊвЛжБНЧБпзїRtЁїECDЃЌЁЯECD=90ЁуЃЌСЌНгBEЃЌADЃЎ
ЃЈ1ЃЉШєCA=CBЃЌCE=CD
ЂйВТЯыЯпЖЮBEЃЌADжЎМфЕФЪ§СПЙиЯЕМАЫљдкжБЯпЕФЮЛжУЙиЯЕЃЌжБНгаДГіНсТлЃЛ
ЂкЯжНЋЭМ1жаЕФRtЁїECDШЦзХЕуCЫГЪБеыа§зЊШёНЧІСЃЌЕУЕНЭМ2ЃЌЧыХаЖЯЂйжаЕФНсТлЪЧЗёШдШЛГЩСЂЃЌШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєCA=8,CB=6ЃЌCE=3ЃЌCD=4ЃЌRtЁїECDШЦзХЕуCЫГЪБеызЊШёНЧІСЃЌШчЭМ3ЃЌСЌНгBDЃЌAEЃЌМЦЫу![]() ЕФжЕЃЎ
ЕФжЕЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЪЧОиаЮЃЌЕу
ЪЧОиаЮЃЌЕу![]() ЁЂ
ЁЂ![]() дкзјБъжсЩЯЃЌ
дкзјБъжсЩЯЃЌ ![]() ЪЧ
ЪЧ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕУЕНЕФЃЌЕу
ЕУЕНЕФЃЌЕу![]() дк
дк![]() жсЩЯЃЌжБЯп
жсЩЯЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕу![]() дк
дк![]() жсЩЯЃЌЦНУцФкЪЧЗёДцдкЕу
жсЩЯЃЌЦНУцФкЪЧЗёДцдкЕу![]() ЃЌЪЙвдЕу
ЃЌЪЙвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮЃПШєДцдкЃЌЧыжБНгаДГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮЃПШєДцдкЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyФкгаШ§ЕуЃКЃЈ0ЃЌЉ2ЃЉЃЌЃЈ1ЃЌЉ1ЃЉЃЌЃЈ2.17ЃЌ0.37ЃЉЃЎдђЙ§етШ§ИіЕу_____ЃЈЬюЁАФмЁБЛђЁАВЛФмЁБЃЉЛвЛИідВЃЌРэгЩЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌ
ЪЧЦНааЫФБпаЮЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФЦНЗжЯпЃЌЧвгыЖдНЧЯп
ЕФЦНЗжЯпЃЌЧвгыЖдНЧЯп![]() ЗжБ№ЯрНЛгкЕу
ЗжБ№ЯрНЛгкЕу![]() .
.

(1)ЧѓжЄ:![]() ЃЛ
ЃЛ
(2)СЌНс![]() ЃЌХаЖЯЫФБпаЮ
ЃЌХаЖЯЫФБпаЮ![]() ЪЧЗёЪЧЦНааЫФБпаЮЃЌЫЕУїРэгЩ.
ЪЧЗёЪЧЦНааЫФБпаЮЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкАыОЖЮЊ5ЕФЩШаЮAOBжаЃЌЁЯAOB=90ЁуЃЌЕуCЪЧЛЁABЩЯЕФвЛИіЖЏЕуЃЈВЛгыЕуAЁЂBжиКЯЃЉODЁЭBCЃЌOEЁЭACЃЌДЙзуЗжБ№ЮЊDЁЂEЃЎ
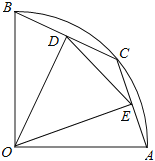
ЃЈ1ЃЉЕБBC=6ЪБЃЌЧѓЯпЖЮODЕФГЄЃЛ
ЃЈ2ЃЉдкЁїDOEжаЪЧЗёДцдкГЄЖШБЃГжВЛБфЕФБпЃПШчЙћДцдкЃЌЧыжИГіВЂЧѓЦфГЄЖШЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
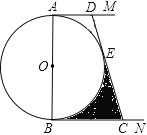
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌAMКЭBNЪЧЁбOЕФСНЬѕЧаЯпЃЌEЮЊЁбOЩЯвЛЕуЃЌЙ§ЕуEзїжБЯпDCЗжБ№НЛAMЃЌBNгкЕуDЃЌCЃЌЧвCB=CEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDA=DEЃЛ
ЃЈ2ЃЉШєAB=6ЃЌCD=4![]() ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНx2Љ6x+mТњзувдЯТЬѕМўЃКЕБЉ2ЃМxЃМЉ1ЪБЃЌЫќЕФЭМЯѓЮЛгкxжсЕФЯТЗНЃЛЕБ8ЃМxЃМ9ЪБЃЌЫќЕФЭМЯѓЮЛгкxжсЕФЩЯЗНЃЌдђmЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com