
 如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点,连接DE.
如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点,连接DE.| AB |
| BC |
| AD |
| AB |
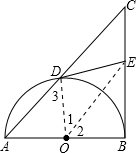 解:(1)连OD,OE,如图,
解:(1)连OD,OE,如图,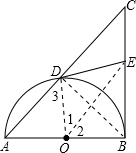
| AB |
| BC |
| AD |
| AB |
| 5 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图是9×7的正方形点阵,其水平方向和竖直方向相邻的两格点间的长度都是1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:
23、如图是9×7的正方形点阵,其水平方向和竖直方向相邻的两格点间的长度都是1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
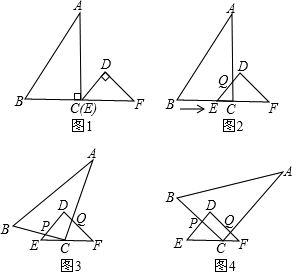 已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013学年浙江省杭州市拱墅区第一学期期末教学质量调研九年级数学试卷(解析版) 题型:解答题
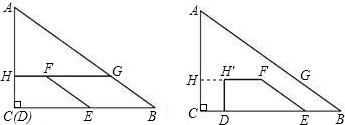
如图, 在Rt△ABC中,∠C=90º, AC=9,BC=12,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ. 点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).

(1)直接用含t的代数式分别表示:QB=__________, PD=___________;
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻成为菱形,求点Q的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com