
 ��ͼ���ı���ABCD��BEFG��Ϊ�����Σ�
��ͼ���ı���ABCD��BEFG��Ϊ�����Σ����� ��1��AG=EC��AG��EC������Ϊ����������BEFG��������ABCD�����������ε����ʵõ����Ա���ȣ�һ��ֱ����ȣ�����SAS�ó�������ABG��������CBEȫ�ȣ�����ȫ�������εĶ�Ӧ����ȣ���Ӧ����ȵõ�CE=AG����BCE=��BAG��������ͬ�ǵ������ȼ��ɵ�֤��
��2����EMB�Ķ���Ϊ45�㣬����Ϊ����B��BP��EC��BH��AM������SAS�ó�������ABG��������BECȫ�ȣ���ȫ�������ε������ȵõ��������������ȣ���AG=EC���ɵó�BP=BH�����õ������߾�����ȵĵ��ڽǵ�ƽ�����ϵõ�BMΪ��ƽ���ߣ����ɡ�BAG=��BCE����һ�ԶԶ�����ȣ��õ���AMCΪֱ�ǣ�����AMEΪֱ�ǣ����ý�ƽ���߶��弴�ɵ�֤��
��3��CM=$\sqrt{2}$BN����AN�Ͻ�ȡNQ=NB���ɵó�������BNQΪ����ֱ�������Σ����õ���ֱ�������ε����ʵõ�BQ=$\sqrt{2}$BN��������֤��BQ=CM����Ҫ֤��������ABQ��������BCMȫ�ȣ�����ͬ�ǵ������ȵõ�һ�Խ���ȣ�����������ANMΪ����ֱ�������εõ�NA=NM�����õ�ʽ�����ʵõ�AQ=BM������SAS�ɵó�ȫ�ȣ�����ȫ�������εĶ�Ӧ����ȼ��ɵ�֤��
��� �⣺��1��AG=EC��AG��EC������Ϊ��
��ͼ1��
��������BEFG��������ABCD��
��GB=BE����ABG=90�㣬AB=BC����ABC=90�㣬
�ڡ�ABG�͡�BEC�У�$\left\{\begin{array}{l}{BG=BE}\\{��ABC=��EBC=90��}\\{BA=BC}\end{array}\right.$��
���ABG�ա�BEC��SAS����
��CE=AG����BCE=��BAG��
�ӳ�CE��AG�ڵ�M��
���BEC=��AEM��
���ABC=��AME=90�㣬
��AG=EC��AG��EC��
��2����EMB�Ķ����������仯����EMB�Ķ���Ϊ45�㣬
������
��ͼ2��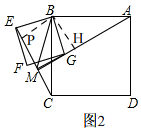
��B��BP��EC��BH��AM��
�ڡ�ABG�͡�CEB�У�
$\left\{\begin{array}{l}{AB=BC}\\{��ABG=��CBE}\\{BG=EB}\end{array}\right.$��
���ABG�ա�CEB��SAS����
��S��ABG=S��EBC��AG=EC��
��$\frac{1}{2}$EC•BP=$\frac{1}{2}$AG•BH��
��BP=BH��
��MBΪ��EMG��ƽ���ߣ�
�ߡ�AMC=��ABC=90�㣬
���EMB=$\frac{1}{2}$��EMG=$\frac{1}{2}$��90��=45�㣻
��3��CM=$\sqrt{2}$BN��
������
��ͼ3��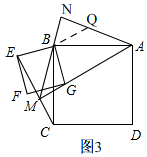
��NA�Ͻ�ȡNQ=NB������BQ��
���BNQΪ����ֱ�������Σ���BQ=$\sqrt{2}$BN��
�ߡ�AMN=45�㣬��N=90�㣬
���AMNΪ����ֱ�������Σ���AN=MN��
��MN-BN=AN-NQ����AQ=BM��
�ߡ�MBC+��ABN=90�㣬��BAN+��ABN=90�㣬
���MBC=��BAN��
�ڡ�ABQ�͡�BCM�У�$\left\{\begin{array}{l}{AQ=BM}\\{��BAN=��MBC}\\{AB=BC}\end{array}\right.$��
���ABQ�ա�BCM��SAS����
��CM=BQ��
��CM=$\sqrt{2}$BN��
�ʴ�Ϊ��CM=$\sqrt{2}$BN��
���� �������ı����ۺ��⣬��Ҫ�����������ε����ʣ�ȫ�������ε��ж������ʣ�����ֱ�������ε��ж������ʣ���ƽ���ߵ��ж����������������ε������ǽⱾ��Ĺؼ�����һ���е��Ѷȵ��п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪��ABC�ĸ�AD����ƽ����AE����B=24�㣬��ACD=56�㣬��ô��AED�Ķ����ǣ�������
��ͼ����֪��ABC�ĸ�AD����ƽ����AE����B=24�㣬��ACD=56�㣬��ô��AED�Ķ����ǣ�������| A�� | 45�� | B�� | 42�� | C�� | 41�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
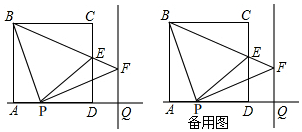
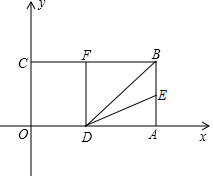 ��ͼ���Գ�����OABC�Ķ���OΪԭ�㣬OA����ֱ��Ϊx�ᣬOC����ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ����֪OA=3��OC=2����E��AB���е㣬��OA��ȡһ��D������BD����A����BD�ĶԳƵ�ǡ�������߶�BC���ϵĵ�F����
��ͼ���Գ�����OABC�Ķ���OΪԭ�㣬OA����ֱ��Ϊx�ᣬOC����ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ����֪OA=3��OC=2����E��AB���е㣬��OA��ȡһ��D������BD����A����BD�ĶԳƵ�ǡ�������߶�BC���ϵĵ�F�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
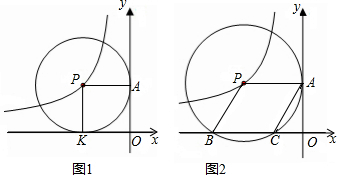
 ��֪������y=-x2+bx+3��x�Ḻ����������A��B���㣬��y�����C����tan��ACO=$\frac{1}{3}$����ABC�����Բ��Բ��ΪM��
��֪������y=-x2+bx+3��x�Ḻ����������A��B���㣬��y�����C����tan��ACO=$\frac{1}{3}$����ABC�����Բ��Բ��ΪM���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com