
 已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.
已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.分析 (1)利用待定系数法直接求出抛物线解析式;
(2)分两种情况用三角形BCP的面积建立方程,解方程即可得出点P的坐标;
(3)先判断出三角形BCQ是直角三角形,进而得出Q是⊙M的直径的一个端点,再分两种情况求出直线交点坐标,进而判定是否相似即可.
解答 解:(1)由tan∠ACO=$\frac{1}{3}$,OC=3,OA=1,
∴A(-1,0)代入解析式得b=2,
∴y=-x2+2x+3;
(2)存在;直线BC的解析式为y=-x+3,
设P(x,-x2+2x+3).
①若P在BC上方的抛物线上,
如图1,
过P作PH⊥x轴交BC于G,
则:S△BCP=$\frac{1}{2}$PG×OB=$\frac{1}{2}$[-x2+2x+3-(-x+3)]×3=-$\frac{3}{2}$x2+$\frac{9}{2}$x,
∵S△BCP=3,
∴-$\frac{3}{2}$x2+$\frac{9}{2}$x=3,
∴x1=1,x2=2,
∴P1(1,4),P2(2,3);
②若P在BC下方的抛物线上,
如图2,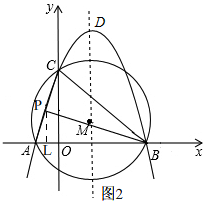
过P作PL⊥x轴于L,
则:S△BCP=S△BOC+S梯形PLOC-S△PLB=$\frac{1}{2}$[OC×OB+(PL+OC)×OL-BL×PL]=$\frac{1}{2}$[3×3+(-x2+2x+3+3)×(-x)-(3-x)×(-x2+2x+3)]=$\frac{1}{2}$(3x2-9x)=3,
∴x=$\frac{3+\sqrt{17}}{2}$(舍)或x=$\frac{3-\sqrt{17}}{2}$,
此时P3($\frac{3-\sqrt{17}}{2}$,$\frac{1+\sqrt{17}}{2}$).
综上P1(1,4),P2(2,3),P3($\frac{3-\sqrt{17}}{2}$,$\frac{1+\sqrt{17}}{2}$).
(3)存在;如图3,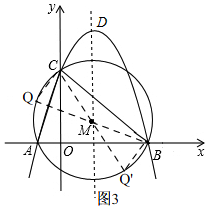
∵抛物线y=-x2+2x+3,
∴B(3,0),
∵C(0,3),
∴BC=3$\sqrt{2}$,直线BC的解析式为y=-x+3,
∴直线BC的垂直平分线的解析式为y=x,
∵AB的垂直平分线是抛物线的对称轴x=1,
∴M(1,1),
∵△AOC是直角三角形,△AOC与△BQC相似,
∴△BQC是直角三角形,
∵BC不是直径,
∴点Q是⊙M的直径的一个端点,
①当∠BCQ是直角,则BQ是直径,
∴CQ⊥BC,
∵C(0,3),
∴直线CQ的解析式为y=x+3①,
∵M(1,1),B(3,0),
∴直线BQ的解析式为y=-$\frac{1}{2}$x+$\frac{3}{2}$②,
联立①②得,x=-1.y=2,
∴Q(-1,2),
∴CQ=$\sqrt{2}$,
∵BC=3$\sqrt{2}$,
∴$\frac{CQ}{BC}=\frac{1}{3}$,
∵tan∠ACO=$\frac{OA}{OC}$=$\frac{1}{3}$,
∴$\frac{OA}{OC}=\frac{CQ}{BC}$,
∵∠AOC=∠QCB=90°,
∴△AOC∽△QCB,
②当∠BQ'C=90°时,同①的方法即可得出Q'(2,-1)
即:满足条件的Q(2,-1),Q'(-1,2).
点评 此题是二次函数综合题,主要考查了待定系数法,三角形的面积公式,直线的交点坐标的求法,相似三角形的性质和判定,解本题的关键是求出直线解析式,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
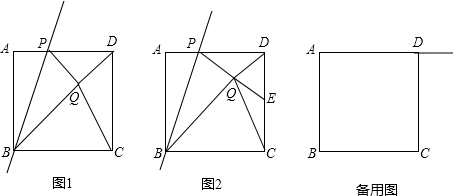
 如图,四边形ABCD、BEFG均为正方形.
如图,四边形ABCD、BEFG均为正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90°,∠ABC=60°,若CD=2,AB=6,则S△ABD=$\frac{9\sqrt{3}}{2}$-3.
如图,在△ABC中,∠C=90°,∠ABC=60°,若CD=2,AB=6,则S△ABD=$\frac{9\sqrt{3}}{2}$-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,三角形纸片ABC中,∠BCA=90°,在AC上取一点E,以BE为折痕进行翻折,使AB的一部分与BC重合,A与BC延长线上的点D重合,若∠A=30°,AC=6,则,DE的长度为( )
如图,三角形纸片ABC中,∠BCA=90°,在AC上取一点E,以BE为折痕进行翻折,使AB的一部分与BC重合,A与BC延长线上的点D重合,若∠A=30°,AC=6,则,DE的长度为( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com