练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，三角形纸片ABC中，∠BCA=90°，在AC上取一点E，以BE为折痕进行翻折，使AB的一部分与BC重合，A与BC延长线上的点D重合，若∠A=30°，AC=6，则，DE的长度为（　　）
    A．6B．4C．3D．2

    分析 先用含30°的直角三角形性质得出BC，进而求出CE，即可求出AE，由折叠的性质即可得出结论．

    解答 解：在Rt△ABC中，∠A=30°，
    ∴BC=2$\sqrt{3}$，∠ABC=60°
    由折叠知，DE=AE，∠DBE=∠ABE=$\frac{1}{2}$∠ABC=30°=∠A，
    在Rt△BCE中，BC=2$\sqrt{3}$，∠DBE=30°，
    ∴CE=2，
    ∴AE=AC-CE=4，
    ∴DE=4，
    故选B．

    点评 此题是折叠问题，主要考查了折叠的性质，含30°的直角三角形的性质，用30°的直角三角形的性质是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

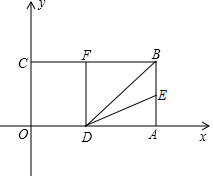    3．如图，以长方形OABC的顶点O为原点，OA所在直线为x轴，OC所在直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，连结BD，点A关于BD的对称点恰好落在线段BC边上的点F处．
    （1）直接写出点E，F的坐标；
    （2）在线段CB上是否存在一点P，使△OEP为等腰三角形？若存在，求出所有满足条件的P点坐标；若不存在，请说明理由．
    （3）在x轴、y轴上是否分别存在点M、N，使四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

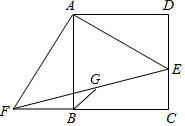    4．E为正方形ABCD的边CD上一点，将△ADE绕A点顺时针旋转90°，得△ABF，G为EF中点．下列结论：①G在△ABF的外接圆上；②EC=$\sqrt{2}$BG；③B，G，D三点在同一条直线上；④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD，那么E为DC的黄金分割点．正确的是（　　）
    A．①②B．①②③C．①③④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点，交y轴与点C，且tan∠ACO=$\frac{1}{3}$，△ABC的外接圆的圆心为M．
    （1）求该二次函数的解析式；
    （2）在x轴上方的抛物线上是否存在一点P，使S△BCP=3，若存在请求出点P坐标，若不存在，说明理由；
    （3）圆上是否存在Q点，使△AOC与△BQC相似？若存在，直接写出点Q坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在平面直角坐标系内，点O为坐标原点，抛物线y=ax2+bx+2交x正半轴 于点A，交x轴负半轴于点B，交y轴于点C，OB=OC，连接AC，tan∠OCA=2．
    （1）求抛物线的解析式；
    （2）点P是第三象限抛物线y=ax2+bx+2上的一个动点，过点P作y轴的平行线交直线AC于点D，设PD的长为d，点P的横坐标为t，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；
    （3）在（2）的条件下，连接PA，PC，当△ACP的面积为30时，将△APC沿AP折叠得△APC′，点C′为点C的对应点，求点C′坐标并判断点C′是否在抛物线y=ax2+bx+2上，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，四边形ABCD中，AD=CD，AB=CB．我们把这种两组邻边分别相等的凸四边形叫做筝形．AC，BD叫作筝形的对角线．请你通过观察、测量、折纸等方法进行探究，并回答以下问题：
    （1）判断下列结论是否正确；
    a．∠DAB=∠DCB；√
    b．∠ABC=∠ADC；× 
    c．BD分别平分∠ABC和∠ADC√
    d．筝形是轴对称图形，它有两条对称轴．×
    （2）请你选择下列问题中的一个进行证明：
    a．从（1）中选择一个正确的结论进行证明；
    b．通过探究，再找到一条筝形的性质，并进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

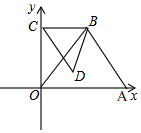    5．如图，直角坐标系中，O为原点，A（6，0），在等腰三角形ABO中，OB=BA=5，点B在第一象限，C（0，k）为y轴正半轴上一动点，作以∠CBD为顶角的等腰三角形CBD，且∠CBD=∠OBA，连结AD．
    （1）①求点B的坐标；②若BD∥OC，求k的值．
    （2）求证：OC=AD；
    （3）设直线AD与y轴交于点M（0，m），当点C在y轴上运动时，点M的位置是否改变？若改变，求m与k的函数关系式，若不变，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在平面直角坐标系xOy中，⊙C的半径为r（r＞1），P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：若直线CP与⊙C交于点A，B，满足|PA-PB|=2，则称点P为⊙C的“完美点”，如图为⊙C及其“完美点”P的示意图．
    （1）当⊙O的半径为2时，
    ①在点M（$\frac{3}{2}$，0），N（0，1），T（-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）中，⊙O的“完美点”是N，T；
    ②若⊙O的“完美点”P在直线y=$\sqrt{3}$x上，求PO的长及点P的坐标；
    （2）⊙C的圆心在直线y=$\sqrt{3}$x+1上，半径为2，若y轴上存在⊙C的“完美点”，求圆心C的纵坐标t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．将二次函数y=$\frac{1}{4}$x2+x-1化为y=a（x+h）2+k的形式是（　　）
    A．y=$\frac{1}{4}（x+2）^{2}+2$B．y=$\frac{1}{4}$（x-2）2-2C．y=$\frac{1}{4}$（x+2）2-2D．y=$\frac{1}{4}$（x-2）2+2

    查看答案和解析>>

    同步练习册答案