Question

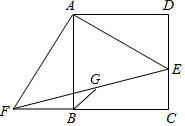
4．E为正方形ABCD的边CD上一点，将△ADE绕A点顺时针旋转90°，得△ABF，G为EF中点．下列结论：①G在△ABF的外接圆上；②EC=$\sqrt{2}$BG；③B，G，D三点在同一条直线上；④若S_{四边形BGEC}=$\frac{1}{4}$S_{正方形ABCD}，那么E为DC的黄金分割点．正确的是（　　）

• A． ①②
• B． ①②③
• C． ①③④
• D． ①②③④

Answer 1

分析 先判断出点A，F，B，G四点共圆即可得出①正确，再用线段的垂直平分线的判定即可得出③正确，进而判断出∠CBD=45°，再判断出GH是△CEF的中位线，判断出，进而用等腰直角三角形的性质得出BG=$\sqrt{2}$BH即可得出②正确，利用S_{四边形BGEC}=$\frac{1}{4}$S_{正方形ABCD}，判断出CE=2DE，即可判断出④错误．

解答 解：∵将△ADE绕A点顺时针旋转90°，得△ABF，
∴∠EAF=90°，
∵G为EF中点．
∴EG=FG，∠AGF=90°，
∵四边形ABCD是正方形，
∴AB=BC=CD=AD，∠ABF=∠ABC=∠ADC=∠BCD=90°，
∴∠AGF=∠ABF=90°，
∴点A，F，B，G四点共圆，
∴点G在△ABF的外接圆上；
所以①正确，
连接AC，在Rt△AEF中，EG=FG，
∴AG=$\frac{1}{2}$EF，
在Rt△CEF中，EG=FG，
∴CG=$\frac{1}{2}$EF，
∴AG=CG，
∴点G是线段AC的垂直平分线上，
∵AB=CB，
∴点B是线段AC的垂直平分线上，
∵AD=CD，
∴点D是线段AC的垂直平分线上，
∴点B，G，D都在线段AC的垂直平分线上，
∴B，G，D三点在同一条直线上；所以③正确，
∵B，G，D三点在同一条直线上；
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=45°，
过点G作GH⊥BC，
∴GH∥CE，
∵EG=FG，
∴GH是△CEF的中位线，
∴CE=2GH，
在Rt△BHG中，∠CBD=45°，
∴BG=$\sqrt{2}$GH，
∴GH=$\frac{\sqrt{2}}{2}$BG，
∴CE=2×$\frac{\sqrt{2}}{2}$BG=$\sqrt{2}$BG，
所以②正确；
∵S_{四边形BGEC}=S_△BHG+S_梯形CEGH
=$\frac{1}{2}$GH²+$\frac{1}{2}$（GH+CE）×CH
=$\frac{1}{2}$GH²+$\frac{1}{2}$（GH+CE）×（BC-GH）
=$\frac{1}{2}$（$\frac{1}{2}$CE）²+$\frac{1}{2}$（$\frac{1}{2}$CE+CE）×（BC-$\frac{1}{2}$CE）
=$\frac{1}{8}$CE²+$\frac{3}{4}$CE×（BC-$\frac{1}{2}$CE）
=$\frac{3}{4}$CE×CD-$\frac{1}{4}$CD²，
S_{正方形ABCD}=CD²，
∵S_{四边形BGEC}=$\frac{1}{4}$S_{正方形ABCD}，
∴$\frac{3}{4}$CE×CD-$\frac{1}{4}$CD²=$\frac{1}{4}$CD²，
∴3CE=2CD=2（CE+DE），
∴CE=2DE，
∴E不是DC的黄金分割点．
所以④错误，
即：正确的有①②③，
故选B．

点评 此题是旋转的性质，主要考查了正方形的性质，四点共圆，直角三角形的斜边的直线等于斜边的一半，等腰直角三角形的性质，几何图形的面积，三角形的中位线．判断出B，G，D三点共线是解本题的关键．