

分析 (1)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形;
(2)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形,再由旋转角是90°,即可得出结论;
(3)由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论.
解答 (1)证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的.
∴DE=AC=AF,∠BAF=α,∠DBE=∠ABC=α,∠DEB=∠C=α,
∴∠DEB=∠BAF,
∴DE∥AF,
∵DE=AF,
∴四边形AFDE是平行四边形,
故答案为:平行四边形;
(2)证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的,
∴∠DBA=∠FAB=90°,DB=AB=AF,
∴∠DBA+∠FAB=180°,
∴DB∥AF,
∵DB=AF,
∴四边形DBAF是平行四边形,
∵∠DBA=90°
∴平行四边形DBAF是正方形.
(3)四边形AEDG是平行四边形.
证明:∵四边形ABDF是正方形,
∴∠DFA=∠DBA=90°,AB=DF
又∵∠DBE=∠AFG=α,
∴∠EBA=∠GFD.
在△ABE和△DFG中,$\left\{\begin{array}{l}{AB=DF}\\{∠EBA=∠GFD}\\{BE=GF}\end{array}\right.$
∴△ABE≌△DFG,
∴AE=DG,
又∵DE=AG=AB,
∴四边形DEAG是平行四边形.
点评 此题是四边形综合题,主要考查了旋转的性质,平行四边形的性质和判定,正方形的判定和性质,全等三角形的判定和性质,掌握旋转的性质和灵活运用旋转的性质是解本题的关键,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
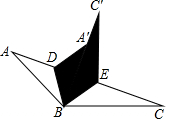 如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.
如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.
已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx与x轴交于点A(4,0),点B(1,3)在抛物线上,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
如图,抛物线y=ax2+bx与x轴交于点A(4,0),点B(1,3)在抛物线上,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:
如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com