
分析 先根据二次根式及分式有意义的条件求出x的值,进而可得出y的值,代入代数式进行计算即可.
解答 解:∵$\sqrt{\frac{3-4x}{2x+1}}$及$\sqrt{\frac{4x-3}{2x+1}}$有意义,
∴$\left\{\begin{array}{l}\frac{3-4x}{2x+1}≥0\\ \frac{4x-3}{2x+1}≥0\\ 2x-1≠0\end{array}\right.$,
解得x=$\frac{3}{4}$,
∴y=1,
∴x+xy+x2y=$\frac{3}{4}$+$\frac{3}{4}$+($\frac{3}{4}$)2=$\frac{33}{16}$.
点评 本题考查的是二次根式有意义的条件,熟知二次根式中的被开方数是非负数是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
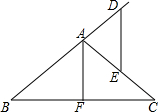 如图,在△ABC中,AB=AC,AF⊥BC,点D在BA的延长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,并证明你的结论.
如图,在△ABC中,AB=AC,AF⊥BC,点D在BA的延长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com