Question

如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为E、F，AE＝AF．

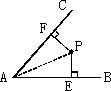
求证：(1)PE＝PF；

(2)点P在∠BAC的平分线上．

Answer 1

答案：
解析：

分析：(1)要证明PE＝PF，考虑利用全等三角形的知识．连接AP，此时可以考虑利用HL证明Rt△AEP≌Rt△AFP，问题即可解决．(2)要证明点P在∠BAC的平分线上，由(1)很快得到∠EAP＝∠FAP，于是即可得解． 　　证明：(1)连接AP． 　　因为PE⊥AB，PF⊥AC， 　　所以∠AEP＝∠AFP＝90°． 　　又因为AE＝AF，AP＝AP， 　　所以Rt△AEP≌Rt△AFP． 　　所以PE＝PF． 　　(2)因为Rt△AEP≌Rt△AFP， 　　所以∠EAP＝∠FAP． 　　所以AP是∠BAC的平分线， 　　即点P在∠BAC的平分线上． 　　点评：解决本题的关键是作辅助线证明三角形全等，从而得出要证明的结论．