
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЖдгкЕу
жаЃЌЖдгкЕу![]() КЭЕу
КЭЕу![]() ИјГіШчЯТЖЈвхЃКШє
ИјГіШчЯТЖЈвхЃКШє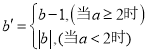 ЃЌдђГЦЕу
ЃЌдђГЦЕу![]() ЮЊЕу
ЮЊЕу![]() ЕФЯоБфЕуЃЎР§ШчЃКЕу
ЕФЯоБфЕуЃЎР§ШчЃКЕу![]() ЕФЯоБфЕуЕФзјБъЪЧ
ЕФЯоБфЕуЕФзјБъЪЧ![]() Еу
Еу![]() ЕФЯоБфЕуЕФзјБъЪЧ
ЕФЯоБфЕуЕФзјБъЪЧ![]() Еу
Еу![]() ЕФЯоБфЕуЕФзјБъЪЧ
ЕФЯоБфЕуЕФзјБъЪЧ![]() ЃЎ
ЃЎ
![]() ЂйЕу
ЂйЕу![]() ЕФЯоБфЕуЕФзјБъЪЧ ЃЛ
ЕФЯоБфЕуЕФзјБъЪЧ ЃЛ
ЂкдкЕу![]() жагавЛИіЕуЪЧЫЋЧњЯп
жагавЛИіЕуЪЧЫЋЧњЯп![]() ЩЯФГвЛИіЕуЕФЯоБфЕуЃЌетИіЕуЪЧ(ЬюЁА
ЩЯФГвЛИіЕуЕФЯоБфЕуЃЌетИіЕуЪЧ(ЬюЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБ)
ЁБ)
![]() ШєЕу
ШєЕу![]() дкЙигк
дкЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФЭМЯѓЩЯЃЌЦфЯоБфЕу
ЕФЭМЯѓЩЯЃЌЦфЯоБфЕу![]() ЕФзнзјБъ
ЕФзнзјБъ![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() Лђ
Лђ![]() Цфжа
Цфжа![]() ЃЎСю
ЃЎСю![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
![]() ШєЕу
ШєЕу![]() дкКЏЪ§
дкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌЦфЯоБфЕу
ЕФЭМЯѓЩЯЃЌЦфЯоБфЕу![]() ЕФзнзјБъ
ЕФзнзјБъ![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЁОД№АИЁП![]() Ђй
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛ
ЃЛ ![]() ЃЛ
ЃЛ ![]() ЕФШЁжЕЗЖЮЇЪБЃК
ЕФШЁжЕЗЖЮЇЪБЃК![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйa=![]() ЃМ2ЃЌЙЪb=
ЃМ2ЃЌЙЪb=![]() =1,ЙЪД№АИЮЊ
=1,ЙЪД№АИЮЊ![]() ЃЛ
ЃЛ
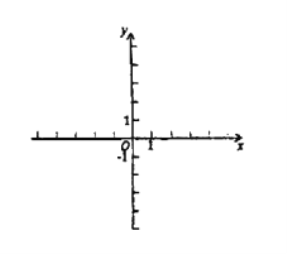
ЂкМйЩшЯоБфЕуA(-2,2)ЖдгІЕФдЕуЮЊЃК(-2,2)Лђ(-2,-2)ЃЌетСНИіЕуЖМВЛдкЗДБШР§КЏЪ§ЭМЯёЩЯЃЛМйЩшЯоБфЕуB(1,3)ЖдгІЕФдЕугІИУЮЊЃК(1,2)ЃЌЕу(1,2)дкЗДБШР§КЏЪ§ЭМЯёЩЯЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉвРЬтвтЃЌ![]() ЭМЯёЩЯЕФЕуPЕФЯоБфЕуQБидкКЏЪ§
ЭМЯёЩЯЕФЕуPЕФЯоБфЕуQБидкКЏЪ§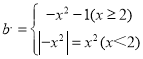 ЕФЭМЯёЩЯЃЌЕБx=2ЪБЃЌy=-4-1=-5ЃЌМДЕуB(2,-5)ЃЌb=-5ЃЌЙЪЕБxЁн2ЪБЃЌb=yЁм-5ЃЌЕБxЃМ2ЪБЃЌy= bЁн0ЃЌm=0ЃЌn=-5ЃЌs=m-n=5ЃЛ
ЕФЭМЯёЩЯЃЌЕБx=2ЪБЃЌy=-4-1=-5ЃЌМДЕуB(2,-5)ЃЌb=-5ЃЌЙЪЕБxЁн2ЪБЃЌb=yЁм-5ЃЌЕБxЃМ2ЪБЃЌy= bЁн0ЃЌm=0ЃЌn=-5ЃЌs=m-n=5ЃЛ
ЃЈ3ЃЉвРЬтвтЃЌy=x-3(-2ЁмxЁмkЃЌkЃО-2)ЭМЯёЩЯЕФЕуPЕФЯоБфЕуQБидкКЏЪ§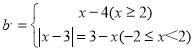 ЕФЭМЯёЩЯЃЌЕБx=2ЪБЃЌbШЁзюаЁжЕЃЌb=2-4=-2ЃЌЕБb=5ЪБЃЌx-4=5Лђ-x+3=5ЃЌЁрx=9Лђx=-2ЃЌЕБb=1ЪБЃЌx-4=1ЃЌx=5ЃЌМДПЩЧѓНт.
ЕФЭМЯёЩЯЃЌЕБx=2ЪБЃЌbШЁзюаЁжЕЃЌb=2-4=-2ЃЌЕБb=5ЪБЃЌx-4=5Лђ-x+3=5ЃЌЁрx=9Лђx=-2ЃЌЕБb=1ЪБЃЌx-4=1ЃЌx=5ЃЌМДПЩЧѓНт.
НтЃКЃЈ1ЃЉЂй a=![]() ЃМ2ЃЌЙЪb=
ЃМ2ЃЌЙЪb=![]() =1,ЙЪД№АИЮЊ
=1,ЙЪД№АИЮЊ![]() ЃЛ
ЃЛ
ЂкМйЩшЯоБфЕуA(-2,2)ЖдгІЕФдЕуЮЊЃК(-2,2)Лђ(-2,-2)ЃЌетСНИіЕуЖМВЛдкЗДБШР§КЏЪ§ЭМЯёЩЯЃЛ
МйЩшЯоБфЕуB(1,3)ЖдгІЕФдЕугІИУЮЊЃК(1,2)ЃЌЕу(1,2)дкЗДБШР§КЏЪ§ЭМЯёЩЯЃЛ
ЙЪД№АИЮЊB.
ЃЈ2ЃЉвРЬтвтЃЌ![]() ЭМЯёЩЯЕФЕуPЕФЯоБфЕуQБидкКЏЪ§
ЭМЯёЩЯЕФЕуPЕФЯоБфЕуQБидкКЏЪ§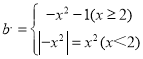 ЕФЭМЯёЩЯЃЈШчЭМ1ЃЉЃЌ
ЕФЭМЯёЩЯЃЈШчЭМ1ЃЉЃЌ
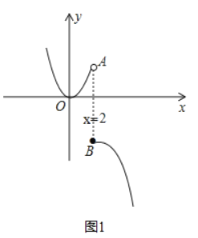
ЕБx=2ЪБЃЌy=-4-1=-5ЃЌМДЕуB(2,-5)ЃЌb=-5ЃЌЙЪЕБxЁн2ЪБЃЌb=yЁм-5ЃЌЕБxЃМ2ЪБЃЌy= bЁн0ЃЌm=0ЃЌn=-5ЃЌs=m-n=5ЃЛ
ЃЈ3ЃЉвРЬтвтЃЌy=x-3(-2ЁмxЁмkЃЌkЃО-2)ЭМЯёЩЯЕФЕуPЕФЯоБфЕуQБидкКЏЪ§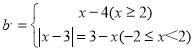

ЕБx=2ЪБЃЌbШЁзюаЁжЕЃЌb=2-4=-2ЃЌ
ЕБb=5ЪБЃЌx-4=5Лђ-x+3=5ЃЌЁрx=9Лђx=-2ЃЌ
ЕБb=1ЪБЃЌx-4=1ЃЌx=5ЃЌ
Ёп-2ЁмbЁм5
ЁргЩЭМЯёжЊЃЌkЕФШЁжЕЗЖЮЇЪЧ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЭМЯѓЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЌЯТСаНсТлЃКЂй2a+bЃН0ЃЛЂк9a+cЃО3bЃЛЂлШєЕуAЃЈЉ3ЃЌy1ЃЉЁЂЕуBЃЈЉ![]() ЃЌy2ЃЉЁЂЕуCЃЈ
ЃЌy2ЃЉЁЂЕуCЃЈ![]() ЃЌy3ЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЌдђy1ЃМy3ЃМy2ЃКЂмШєЗНГЬax2+bx+cЃНЉ3ЃЈaЁй0ЃЉЕФСНИљЮЊx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђx1ЃМЉ1ЃМ3ЃМx2ЃЛЂнmЃЈam+bЃЉЉbЃМaЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
ЃЌy3ЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЌдђy1ЃМy3ЃМy2ЃКЂмШєЗНГЬax2+bx+cЃНЉ3ЃЈaЁй0ЃЉЕФСНИљЮЊx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђx1ЃМЉ1ЃМ3ЃМx2ЃЛЂнmЃЈam+bЃЉЉbЃМaЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ

A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвдЦНааЫФБпаЮABCDЕФНЯЖЬБпCDЮЊвЛБпзїСтаЮCDEFЃЌЪЙЕуFТфдкБпADЩЯЃЌСЌНгBEЃЌНЛAFгкЕуGЃЌбгГЄDEЃЌBAНЛгкЕуHЃЌШєЁЯADC=60ЁуЃЌдђ![]() =________
=________
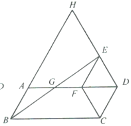
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКсзјБъКЭзнзјБъЖМЪЧећЪ§ЕФЕуНазїећЕуЃЌКЏЪ§y=![]() ЕФЭМЯѓЩЯЕФећЕуЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
ЕФЭМЯѓЩЯЕФећЕуЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 3Иі B. 4Иі C. 6Иі D. 8Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСгыгІгУЃКЭЌбЇУЧЃЌФуУЧвбОжЊЕР![]() ЃЌМД
ЃЌМД![]() ЃЎЫљвд
ЃЎЫљвд![]() ЃЈЕБЧвНіЕБ
ЃЈЕБЧвНіЕБ![]() ЪБШЁЕШКХЃЉЃЎ
ЪБШЁЕШКХЃЉЃЎ
дФЖС1ЃКШє![]() ЮЊЪЕЪ§ЃЌЧв
ЮЊЪЕЪ§ЃЌЧв![]() ЃЈЕБЧвНіЕБ
ЃЈЕБЧвНіЕБ![]() ЪБШЁЕШКХЃЉЃЎ
ЪБШЁЕШКХЃЉЃЎ
дФЖС2ЃКШєКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊГЃЪ§ЃЉЃЎгЩдФЖС1НсТлПЩжЊЃК
ЮЊГЃЪ§ЃЉЃЎгЩдФЖС1НсТлПЩжЊЃК![]() МД
МД![]() ЃЌЁрЕБ
ЃЌЁрЕБ![]() МД
МД![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
дФЖСРэНтЩЯЪіФкШнЃЌНтД№ЯТСаЮЪЬтЃК
ЮЪЬт1ЃКШєКЏЪ§![]() ЃЌдђ
ЃЌдђ![]() = ЪБЃЌКЏЪ§
= ЪБЃЌКЏЪ§![]() ЕФзюаЁжЕЮЊ ЃЎ
ЕФзюаЁжЕЮЊ ЃЎ
ЮЪЬт2ЃКвбжЊвЛИіОиаЮЕФУцЛ§ЮЊ4ЃЌЦфжавЛБпГЄЮЊ![]() ЃЌдђСэвЛБпГЄЮЊ
ЃЌдђСэвЛБпГЄЮЊ![]() ЃЌжмГЄЮЊ
ЃЌжмГЄЮЊ![]() ЃЌЧѓЕБ
ЃЌЧѓЕБ![]() ЪБЃЌОиаЮжмГЄЕФзюаЁжЕЮЊ ЃЎ
ЪБЃЌОиаЮжмГЄЕФзюаЁжЕЮЊ ЃЎ
ЮЪЬт3ЃКЧѓДњЪ§ЪН![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ЮЪЬт4ЃКНЈдьвЛИіШнЛ§ЮЊ8СЂЗНУзЃЌЩю2УзЕФГЄЗНЬхЮоИЧЫЎГиЃЌГиЕзКЭГиБкЕФдьМлЗжБ№ЮЊУПЦНЗНУз![]() УзЃЌЫЎГизмдьМлЮЊ
УзЃЌЫЎГизмдьМлЮЊ![]() ЃЈдЊЃЉЃЌЧѓЕБ
ЃЈдЊЃЉЃЌЧѓЕБ![]() ЮЊЖрЩйЪБЃЌЫЎГизмдьМл
ЮЊЖрЩйЪБЃЌЫЎГизмдьМл![]() зюЕЭЃПзюЕЭЪЧЖрЩйЃП
зюЕЭЃПзюЕЭЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЙцЖЈЃЌвдЖўДЮКЏЪ§y=ax2+bx+cЕФЖўДЮЯюЯЕЪ§aЕФ2БЖЮЊвЛДЮЯюЯЕЪ§ЃЌвЛДЮЯюЯЕЪ§bЮЊГЃЪ§ЯюЙЙдьЕФвЛДЮКЏЪ§y=2ax+bНазіЖўДЮКЏЪ§y=ax2+bx+cЕФЁАзгКЏЪ§ЁБЃЌЗДЙ§РДЃЌЖўДЮКЏЪ§y=ax2+bx+cНазівЛДЮКЏЪ§y=2ax+bЕФЁАФИКЏЪ§ЁБЃЎ
ЃЈ1ЃЉШєвЛДЮКЏЪ§y=2x-4ЪЧЖўДЮКЏЪ§y=ax2+bx+cЕФЁАзгКЏЪ§ЁБЃЌЧвЖўДЮКЏЪ§ОЙ§ЕуЃЈ3ЃЌ0ЃЉЃЌЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНМАЖЅЕузјБъЃЎ
ЃЈ2ЃЉШєЁАзгКЏЪ§ЁБy=x-6ЕФЁАФИКЏЪ§ЁБЕФзюаЁжЕЮЊ1ЃЌЧѓЁАФИКЏЪ§ЁБЕФКЏЪ§БэДяЪНЃЎ
ЃЈ3ЃЉвбжЊЖўДЮКЏЪ§y=-x2-4x+8ЕФЁАзгКЏЪ§ЁБЭМЯѓжБЯпlгыxжсЁЂyжсНЛгкCЁЂDСНЕуЃЌЖЏЕуPЮЊЖўДЮКЏЪ§y=-x2-4x+8ЖдГЦжсгвВрЩЯЕФЖЏЕуЃЌЧѓЁїPCDЕФУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкABCDжаЃЌвбжЊABЃН6ЃЌBEЦНЗжЁЯABCНЛADБпгкЕуEЃЌЕуEНЋADЗжЮЊ1ЃК3СНВПЗжЃЌдђADЕФГЄЮЊЃЈЁЁЁЁЃЉ
A. 8Лђ24B. 8C. 24D. 9Лђ24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊдЕуЃЌХзЮяЯп
ЮЊдЕуЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌЕу
ЃЌЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕуЮЊЕу
ЕФЖдГЦЕуЮЊЕу![]() .Й§Еу
.Й§Еу![]() зїжБЯп
зїжБЯп![]() жсЃЌНЛ
жсЃЌНЛ![]() жсгкЕу
жсгкЕу![]() .
.
ЃЈЂёЃЉЧѓИУХзЮяЯпЕФНтЮіЪНМАЖдГЦжсЃЛ
ЃЈЂђЃЉЕу![]() дк
дк![]() жсЩЯЃЌЕБ
жсЩЯЃЌЕБ![]() ЕФжЕзюаЁЪБЃЌЧѓЕу
ЕФжЕзюаЁЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈЂѓЃЉХзЮяЯпЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌШєДцдкЃЌЧѓГіЕу
ЃЌШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDЕФЖЅЕуAЁЂDЗжБ№ТфдкxжсЁЂyжсЃЌOD=2OA=6ЃЌADЃКAB=3ЃК1ЃЎдђЕуBЕФзјБъЪЧ_______ЃЎ
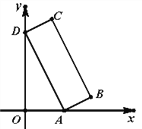
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com