
【题目】如图,在![]() 中,
中,![]() .将
.将![]() 向上翻折,使点
向上翻折,使点![]() 落在
落在![]() 上,记为点
上,记为点![]() ,折痕为
,折痕为![]() ,再将
,再将![]() 以
以![]() 为对称轴翻折至
为对称轴翻折至![]() ,连接
,连接![]() .
.
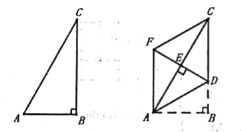
(1)证明:![]()
(2)猜想四边形![]() 的形状并证明.
的形状并证明.
【答案】(1)见解析;(2)四边形ADCF为菱形,证明见解析.
【解析】
(1)根据翻折的性质,先得出AB=AE,∠AED=90°,再根据AC=2AB,可得出DE垂直平分AC,从而可得出结论;
(2)根据折叠的性质以及等边对等角,先求出∠1=∠2=∠3=∠4=30°,从而可得出∠FAB=90°,进而推出AF∥CD,再由边的等量关系,可证明四边形ADCF为菱形.
(1)证明:由轴对称得性质得,
∠B=90°=∠AED,AE=AB,
∵AC =2AB,
∴ED为AC的垂直平分线,
∴AD=CD;
(2)解:四边形ADCF为菱形.证明如下:
∵AD=CD,∴∠1=∠2.
由轴对称性得,
∠1=∠3,∠1=∠4.
∵∠B=90°,
∴∠1=∠2=∠3=∠4=30°,
∴∠FAB=90°,
∴AF∥CD,AF=AD=CD,
∴四边形ADCF为菱形.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
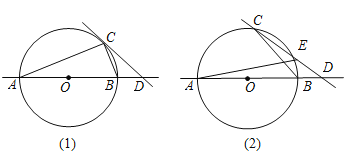
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E,BD:DE:EC=2;3:5求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现在C,D,E三点中,其中一点是另两点连线的中点的情况,问这样的情况出现几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
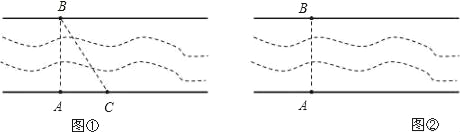
【题目】经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
(1)求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
(2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.(不用考虑计算问题,叙述清楚即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
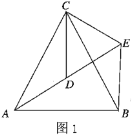
【题目】综合与实践
问题情境
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ;
;
探究发现
(1)善思组发现:![]() ,请你帮他们写出推理过程;
,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了![]() 度数,请直接写出
度数,请直接写出![]() 等于______度;
等于______度;
(3)奋进组在前面两组的基础上又探索出了![]() 与
与![]() 的位置关系为______(请直接写出结果);
的位置关系为______(请直接写出结果);
拓展探究
(4)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() ,试探究
,试探究![]() ,
,![]() ,
,![]() 之间有怎样的数量关系.
之间有怎样的数量关系.
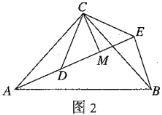
创新组类比善思组的发现,很快证出![]() ,进而得出
,进而得出![]() .请你写出
.请你写出![]() ,
,![]() ,
,![]() 之间的数量关系并帮创新组完成后续的证明过程.
之间的数量关系并帮创新组完成后续的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个带有进水管和出水管的容器,每分钟进、出水量都是一定的,设从某一时刻开始的4分钟内只进水,不出水,在随后的8分钟内既进水又出水,得到 时间x(分)与水量y(升)之间的关系图.(如图)
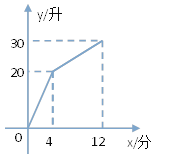
(1)每分钟进水多少?
(2)0<x≤4时,y与x的函数关系式是什么?
(3)4<x≤12时,y与x的函数关系式是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱护环境越来越受到社会各界的重视,为了让学生了解环保知识,某中学组织全校![]() 名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分
名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分![]() 分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
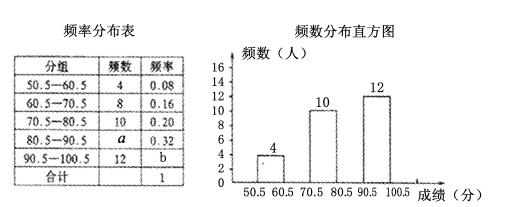
请根据以上的统计图、表解答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)成绩在![]() 分以上(不含
分以上(不含![]() 分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD分别与半圆OO切于点A,D,BC切⊙O于点E.若AB=4,CD=9,则⊙O的半径为( )
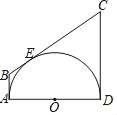
A. 12 B. ![]()
![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com