
【题目】综合与实践
问题情境
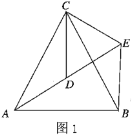
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ;
;
探究发现
(1)善思组发现:![]() ,请你帮他们写出推理过程;
,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了![]() 度数,请直接写出
度数,请直接写出![]() 等于______度;
等于______度;
(3)奋进组在前面两组的基础上又探索出了![]() 与
与![]() 的位置关系为______(请直接写出结果);
的位置关系为______(请直接写出结果);
拓展探究
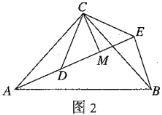
(4)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() ,试探究
,试探究![]() ,
,![]() ,
,![]() 之间有怎样的数量关系.
之间有怎样的数量关系.
创新组类比善思组的发现,很快证出![]() ,进而得出
,进而得出![]() .请你写出
.请你写出![]() ,
,![]() ,
,![]() 之间的数量关系并帮创新组完成后续的证明过程.
之间的数量关系并帮创新组完成后续的证明过程.
【答案】(1)证明见解析;(2)60;(3)![]() ;(4)
;(4)![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据等边三角形的性质可得![]() ,
,![]() ,
,![]() ,利用角的和差关系可得
,利用角的和差关系可得![]() ,利用SAS可证明
,利用SAS可证明![]() ;
;
(2)由外角性质可得∠ADC=120°,根据全等三角形的性质可得∠BEC=∠ADC=120°,进而可得∠AEB的度数;
(3)由∠CDE=∠AEB=60°,即可得出CD//BE;
(4)根据等腰直角三角形的性质可得DE=2CM,根据AD=BE,AE=AD+DE即可得答案.
(1)∵![]() 和
和![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即:
,即:![]() ,
,
在![]() 和
和![]() 中
中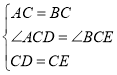 ,
,
∴![]()
(2)∵△DCE是等边三角形,
∴∠DCE=∠DEC=60°,
∴∠ADC=∠DCE+∠DEC=120°,
由(1)得△ACD≌△BCE,
∴∠ADC=∠BEC=120°,
∴∠AEB=∠BEC-∠DEC=60°,
故答案为:60
(3)∵∠CDE=∠AEB=60°,
∴![]() ,
,
故答案为:CD//BE
(4)![]() ,证明如下:
,证明如下:
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
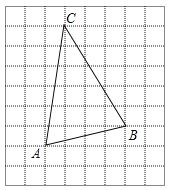
【题目】(2017天津)如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AB的长等于____;
(2)在△ABC的内部有一点P,满足S△PS△PS△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如表(单位:cm).
甲 | 9 | 10 | 11 | 12 | 7 | 13 | 10 | 8 | 12 | 8 |
乙 | 8 | 13 | 12 | 11 | 10 | 12 | 7 | 7 | 9 | 11 |
小颖已求得![]() 甲=10cm,S甲2=3.6(cm2).问:哪种农作物的10株苗长得比较整齐?
甲=10cm,S甲2=3.6(cm2).问:哪种农作物的10株苗长得比较整齐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在两地![]() 之间有汽车站
之间有汽车站![]() 站,客车由
站,客车由![]() 地驶往
地驶往![]() 站,货车由
站,货车由![]() 地驶往
地驶往![]() 地两车同时出发,匀速行驶图2是客车、货车离
地两车同时出发,匀速行驶图2是客车、货车离![]() 站的路程
站的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数关系图像.
(小时)之间的函数关系图像.
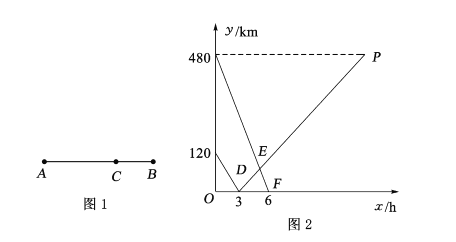
(1)填空:![]() 两地相距 千米;货车的速度是 千米/时;
两地相距 千米;货车的速度是 千米/时;
(2)求三小时后,货车离![]() 站的路程
站的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)试求客车与货两车何时相距![]() 千米?
千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
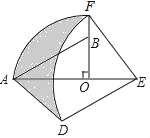
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com