
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

科目:初中数学 来源: 题型:
【题目】“丰收1号”小麦的试验田是边长为![]() 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(
米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(![]() )米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
)米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A,B,C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P,A,B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α
(1)用含α的式子表示h(不必指出α的取值范围);
(2)用含α的式子表示h(不必指出α的取值范围);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB与 x 轴,y 轴分别交于点 A和点 B,点 A的坐标为(1,0),且 2OA=OB.
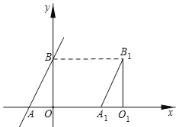
(1)求直线 AB 解析式;
(2)如图,将△A O B 向右平移 3 个单位长度,得到△A1O1B1,求线段 O B1的长;
(3)在(2)中△AOB 扫过的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com