练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知MB=ND，∠MBA=∠NDC，下列哪个条件不能判定△ABM≌△CDN（ ）

    A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N

    【答案】A

    【解析】

    三角形全等的判定定理有：边角边、角角边、角边角和边边边定理，逐项分析即可判断；

    解：A、MB=ND，AM=CN ，∠MBA=∠NDC，△ABM和△CDN不一定全等，错误，符合题意；

    B、∵MB=ND，AM=CN ，AB=CD ，∴△ABM≌△CDN（SSS）， 正确，不符合题意；

    C、∵ AM∥CN，∴∠A=∠NCD，又∠MBA=∠NDC，MB=ND，∴△ABM≌△CD（AAS）， 正确，不符合题意；

    D、∵∠M=∠N，MB=ND，∠MBA=∠NDC，∴△ABM≌△CDN（ASA），正确，不符合题意；

    故答案为：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一架方梯AB长25米，如图所示，斜靠在一面上：

    （1）若梯子底端离墙7米，这个梯子的顶端距地面有多高？

    （2）在（1）的条件下，如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉，经市场调查，甲种花卉的种植费用y（元）与种植面积x（m2）之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元．

    （1）直接写出当0≤x≤300和x＞300时，y与x的函数关系式；

    （2）广场上甲、乙两种花卉的种植面积共1200m2，若甲种花卉的种植面积不少于200m2，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少？最少总费用为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆出租车从超市（点）出发，向东走到达小李家（点），继续向东走到达小张家（点），然后又回头向西走到达小陈家（点），最后回到超市．

    （1）以超市为原点，向东方向为正方向，用表示，画出数轴，并在该数轴上表示、、、的位置；

    （2）小陈家（点）距小李家（点）有多远？

    （3）若出租车收费标准如下，以内包括收费元，超过部分按每千米元收费，则从超市出发到回到超市一共花费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形气旋风暴，有极强的破坏力，此时某台风中心在海域B处，在沿海城市A的正南方向240千米，其中心风力为12级，每远离台风中心25千米，台风就会减弱一级，如图所示，该台风中心正以20千米/时的速度沿北偏东30°方向向C移动，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响． 试问：

    （1）A城市是否会受到台风影响？请说明理由．

    （2）若会受到台风影响，那么台风影响该城市的持续时间有多长？

    （3）该城市受到台风影响的最大风力为几级？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某花店准备购进甲、乙两种花卉，若购进甲种花卉20盆，乙种花卉50盆，需要900元；若购进甲种花卉40盆，乙种花卉30盆，需要960元．

    （1）求购进甲、乙两种花卉每盆各需多少元？

    （2）该花店购进甲，乙两种花卉共100盆，甲种花卉每盆售价20元，乙种花齐每盆售价16元，现该花店把100盆花卉全部售出，若获利超过480元，则至少购进甲种花卉多少盆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，连接BD．
    （1）如图1，AE⊥BD于E．直接写出∠BAE的度数．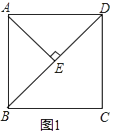

    （2）如图1，在（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°后得到△AB′E′，AB′与BD交于M，AE′的延长线与BD交于N．
    ①依题意补全图1；
    ②用等式表示线段BM、DN和MN之间的数量关系，并证明．
    （3）如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF分别与BD交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）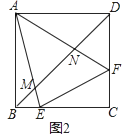

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx+b与反比例函数y= 交于A（﹣1，2），B（2，n），与y轴交于C点．
    （1）求反比例函数和一次函数解析式；
    （2）如图1，若将y=kx+b向下平移，使平移后的直线与y轴交于F点，与双曲线交于D，E两点，若S△ABD=3，
    求D，E的坐标．

    （3）如图2，P为直线y=2上的一个动点，过点P作PQ∥y轴交直线AB于Q，交双曲线于R，若QR=2QP，求P点坐标．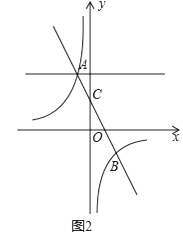

    查看答案和解析>>

    同步练习册答案