
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.

【答案】(1)楼房的高度约为17.3米;(2)当α=45°时,老人仍可以晒到太阳.理由见解析.
【解析】试题分析:(1)在Rt△ABE中,根据![]() 的正切值即可求得楼高;(2)当
的正切值即可求得楼高;(2)当![]() 时,从点B射下的光线与地面AD的交点为F,与MC的交点为点H.可求得AF=AB=17.3米,又因CF=CH=17.3-17.2=0.1米,CM=0.2,所以大楼的影子落在台阶MC这个侧面上.即小猫仍可晒到太阳.
时,从点B射下的光线与地面AD的交点为F,与MC的交点为点H.可求得AF=AB=17.3米,又因CF=CH=17.3-17.2=0.1米,CM=0.2,所以大楼的影子落在台阶MC这个侧面上.即小猫仍可晒到太阳.
试题解析:解:(1)当当![]() 时,在Rt△ABE中,
时,在Rt△ABE中,
∵![]() ,
,
∴BA=10tan60°=![]() 米.
米.
即楼房的高度约为17.3米.

当![]() 时,小猫仍可晒到太阳.理由如下:
时,小猫仍可晒到太阳.理由如下:
假设没有台阶,当![]() 时,从点B射下的光线与地面AD的交点为F,与MC的交点为点H.
时,从点B射下的光线与地面AD的交点为F,与MC的交点为点H.
∵∠BFA=45°,
∴![]() ,此时的影长AF=BA=17.3米,
,此时的影长AF=BA=17.3米,
所以CF=AF-AC=17.3-17.2=0.1.
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上.
∴小猫仍可晒到太阳.


科目:初中数学 来源: 题型:
【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
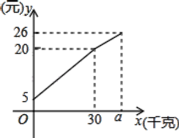
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当t=0.5时,求线段QM的长;
(2)当M在AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形?若可以,请求t的值;若不可以,请说明理由.
(3)当t>2时,连接PQ交线段AC于点R.请探究![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”、“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得 元购物券,至多可得 元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com