
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”、“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得 元购物券,至多可得 元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
【答案】(1)10;80 (2)![]()
【解析】分析:(1)根据题意即可求得该顾客至少可得的购物券,至多可得的购物券的金额;(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与该顾客所获购物券的金额不低于50元的情况,再利用概率公式求解即可求得答案.
本题解析:.(1)10,80;(2)![]()
(2)方法一:树状图法:
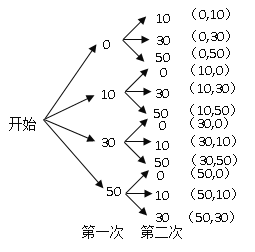
方法二:列表法:
0 | 10 | 30 | 50 | |
0 | (0,10) | (0,30) | (0,50) | |
10 | (10,0) | (10,30) | (10,50) | |
30 | (30,0) | (30,10) | (30,50) | |
50 | (50,0) | (50,10) | (50,30) |
从上面的树状图或表格可以看出,两次摸球可能出现的结果共有12种,
每种结果出现的可能性相同,而所获购物券的金额不低于50元的结果
共有6种.
所以该顾客所获购物券的金额不低于50元的概率是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
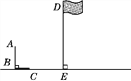
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠A=30°,∠C=40°,求∠AEC的度数.小明的思路是:

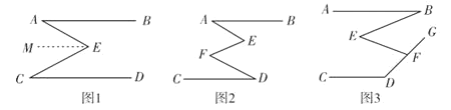
(1)初步尝试:按小明的思路,求得∠AEC的度数;
(2)问题迁移:如图2,AB∥CD,点E、F为AB、CD内部两点,问∠A、∠E、∠F和∠D之间有何数量关系?请说明理由;
(3)应用拓展:如图3,AB∥CD,点E、F为AB、CD内部两点,如果∠E+∠EFG=160°,请直接写出∠B与∠D之问的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间福州一中初中部举行了“宅家运动会”.该学校七、八年级各有300名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取20名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级: | 74 | 97 | 96 | 72 | 98 | 99 | 72 | 73 | 76 | 74 |
74 | 69 | 76 | 89 | 78 | 74 | 99 | 97 | 98 | 99 | |
八年级: | 76 | 88 | 96 | 89 | 78 | 94 | 89 | 94 | 95 | 50 |
89 | 68 | 65 | 89 | 77 | 86 | 89 | 88 | 92 | 91 |
整理数据如下:
|
|
|
|
| |
七年级 | 0 | 1 | 10 | 1 | a |
八年级 | 1 | 2 | 3 | 8 | 6 |
分析数据如下:
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84.2 | 77 | 74 | 138.56 |
八年级 | 84 | b | 89 | 129.7 |
根据以上信息,回答下列问题:
(1)![]() ___________,
___________,![]() ___________;
___________;
(2)你认为哪个年级“宅家运动会”的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性)
(3)学校对“宅家运动会”成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有___________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M和点P(点P在M内部或M上),给出如下定义:
中的图形M和点P(点P在M内部或M上),给出如下定义:
如果图形M上存在点Q,使得![]() ,那么称点P为图形M的和谐点.
,那么称点P为图形M的和谐点.
已知点![]() ,
,![]() ,
,![]() ,
,![]() .
.
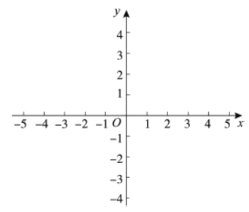
(1)在点![]() ,
,![]() ,
,![]() 中,矩形
中,矩形![]() 的和谐点是_________________;
的和谐点是_________________;
(2)如果直线![]() 上存在矩形
上存在矩形![]() 的和谐点P,求出点P的横坐标t的取值范围;
的和谐点P,求出点P的横坐标t的取值范围;
(3)如果直线![]() 上存在矩形
上存在矩形![]() 的和谐点E,F,使得线段
的和谐点E,F,使得线段![]() 上的所有点(含端点)都是矩形
上的所有点(含端点)都是矩形![]() 的和谐点,且
的和谐点,且![]() ,求出b的取值范围.
,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
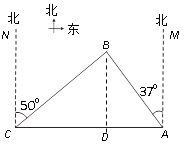
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com