
����Ŀ�������龳����ͼ1��AB��CD����A=30�㣬��C=40�㣬���AEC�Ķ���.С����˼·�ǣ�

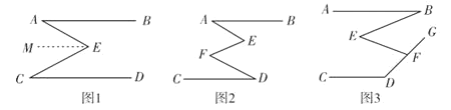
��1���������ԣ���С����˼·����á�AEC�Ķ�����
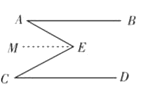
��2������Ǩ�ƣ���ͼ2��AB��CD����E��FΪAB��CD�ڲ����㣬�ʡ�A����E����F�͡�D֮���к�������ϵ?��˵�����ɣ�
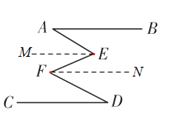
��3��Ӧ����չ����ͼ3��AB��CD����E��FΪAB��CD�ڲ����㣬�����E+��EFG=160�㣬��ֱ��д����B���D֮�ʵ�������ϵ.
���𰸡���1��70�� ��2���𰸼����� ��3����B+��D=160��
��������
��1�����Ӹ����ߣ�ת������ͼ�Σ���E��EM��AB������ƽ���ߵ����ʿ�֤�á�A =��AEM����C=��CEM����֤����AEC=��A+��C���̶��ɽ�����⣻
��2�����Ӹ����ߣ�ת����ֱ��ƽ�еĻ���ͼ�Σ�����E��EM��AB, ����F��FN��AB ������ƽ���ߵ����ʿ�֤AB��ME��FN��CD�� �ٸ�����ֱ��ƽ�У��ڴ�����ȣ���֤�á�A =��AEM����MEF=��EFN,��D=��DFN��Ȼ����ʽ��ӣ���֤�ý��ۣ�
��3������E��EH��AB������F��FM��AB �������֪��֤��AB��CD��FM��EH��������ֱ��ƽ�У�ͬλ����ȣ�ͬ���ڽǻ�������֤��B=��BEH����EFM=��HEF����MFD+��D=180�㣬�ٽ�������ʽ��ӣ������ɵõ���B+��D=180��+��BEF-��EFD��Ȼ���ɡ�BEF+��EFG=160�� �����Ƴ���BEF-��EFD=-20�㣬������������B+��D��ֵ.
��1����ͼ����E��EM��AB��
��AB��CD����AB��ME��CD��
���A =��AEM����C=��CEM��
���AEC=��A+��C=70�㣻
��2����A+��EFD =��AEF+��D
�������£�����E��EM��AB, ����F��FN��AB
��AB��CD����AB��ME��FN��CD��
���A =��AEM����MEF=��EFN,��D=��DFN��
���A+��EFD =��AEF+��D��
��3������E��EH��AB������F��FM��AB ��

��AB��CD��
��AB��CD��FM��EH��
���B=��BEH����EFM=��HEF����MFD+��D=180�㣬
���B+��EFM+��MFD+��D=180��+��BEH+��HEF��
���B+��D+��EFD=180��+��BEF��
���B+��D=180��+��BEF-��EFD��
�� ��BEF+��EFG=160�� ��
���BEF+180��-��EFD=160�㣬
���BEF-��EFD=-20�㣬
���B+��D=180��-20��=160��.


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2013���Ĵ��ϳ�3�֣���ͼ���Ѿ���ABCD��EF���ۣ���Bǡ������AD�ߵ�B�䴦����AE=2��DE=6����EFB=60�㣬�����ABCD������ǡ� ��

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר���꾭��ij���ͺŵ���������֪���ͺ������Ľ���Ϊ15��Ԫ/��������һ��ʱ����֣������ͺ������ۼ۶�Ϊ25��Ԫ/��ʱ��ƽ��ÿ���۳�8�����ۼ�ÿ����0.5��Ԫ��ƽ��ÿ�ܶ��۳�1����
��1�����ۼ�Ϊ22��Ԫ/��ʱ����ƽ��ÿ�ܵ���������
��2�����õ�ƻ�ƽ��ÿ�ܵ�����������90��Ԫ��Ϊ�˾�����ٿ�棬��ÿ���������ۼۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���BAD��80�㣬AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�F��EΪ���㣬����DF�����CDF����(����)
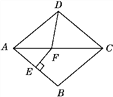
A. 80�� B. 70�� C. 65�� D. 60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶ������������ij߹���ͼ���̣���֪��![]()
����������![]()
��������ͼ��
�����߶�![]() �Ĵ�ֱƽ���߽ǽ�
�Ĵ�ֱƽ���߽ǽ�![]() �ڵ�
�ڵ�![]() ��
��
������![]() ���ӳ������ӳ����Ͻ�ȡ
���ӳ������ӳ����Ͻ�ȡ![]()
������![]()
�����ı���![]() ��Ϊ�������ľ���
��Ϊ�������ľ���
����С����Ƶij߹���ͼ����
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2������±ߵ�֤����
֤����![]() ��
��![]() ��
��
![]() �ı�����ƽ���ı��Σ� ���������������ݣ�
�ı�����ƽ���ı��Σ� ���������������ݣ�
![]()
![]() �ı���
�ı���![]() �Ǿ��Σ� ���������������ݣ�
�Ǿ��Σ� ���������������ݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ѵ�ڼ������٣�Ϊ����ҹ��鿴��ˮ�������ӵ̵��������Ѵָ�Ӳ���һΣ�յش�������������һ̽�յ�(��ͼ1)����BAN=45��.��A������AM˳ʱ����ת��AN��������ת����B������BP˳ʱ����ת��BQ��������ת�����Ʋ�ͣ��������Ѳ��.����Aת�����ٶ���3�ȣ��룬��Bת�����ٶ���1�ȣ���.�ٶ���һ�����������ӵ���ƽ�еģ���PQ��MN.��ͼ2������ͬʱת�����ڵ�A���ߵ���AN֮ǰ.������Ĺ������ڵ�C����C��CD��AC��PQ�ڵ�D������ת�������У����BAC���BCD�ı�ֵ����˵������.
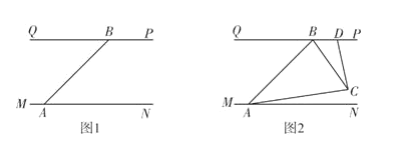
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ������һ�ִ����.��һ�����������������4����ȫ��ͬ��С�����Ϸֱ������0Ԫ������10Ԫ������30Ԫ������50Ԫ��������.�涨���˿��ڱ��̳�ͬһ���ڣ�����ÿ��300Ԫ���Ϳ��Դ��������Ⱥ�����������ÿ��ֻ����һ����һ�������Żأ�.�̳���������С��������֮�ͷ�����Ӧ�۸�Ĺ���ȯ�����������ڱ��̳�����.ij�˿����Ѹպ���300Ԫ�����ڱ���������:
(1)�ù˿����ٿɵ� Ԫ����ȯ������ɵ� Ԫ����ȯ;
(2)���û���״ͼ���б���������ù˿�������ȯ�Ľ�����50Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y=![]() ��ͼ����һ�κ���y=kx+b��ͼ���ڵ�A��m��2������B����2��n ����һ�κ���ͼ����y��Ľ���ΪC��
��ͼ����һ�κ���y=kx+b��ͼ���ڵ�A��m��2������B����2��n ����һ�κ���ͼ����y��Ľ���ΪC��
��1����һ�κ�������ʽ��
��2����C������ꣻ
��3������AOB�������
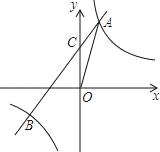
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���μκ���������һ�����dz��о���ѧ���⣺
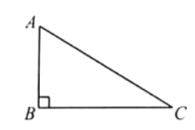
һ�����dz߷ֱ���һ����Ϊֱ�ǣ�����Ƕ���ͼ1��ʾ��![]() .
.
���֣�
(1)��ͼ2����![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() _____.
_____.
(2)��ͼ3����ͼ2��![]() ��
��![]() ��˳ʱ����תһ���Ƕ�ʹ��
��˳ʱ����תһ���Ƕ�ʹ��![]() ����
����![]() �Ķ���.
�Ķ���.
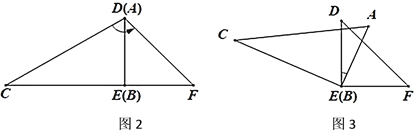
��չ��
(3)��ͼ4��������ת��ʹ��![]() �ڵ�
�ڵ�![]() ��
��
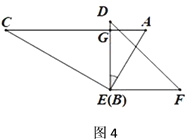
�ٴ�ʱ![]() ��
��![]() ƽ������˵������.
ƽ������˵������.
����![]() �Ķ���.
�Ķ���.
̽����
(4)��ͼ5��ͼ6��������ת��ʹ��![]() ����
����![]() �Ķ���.
�Ķ���.
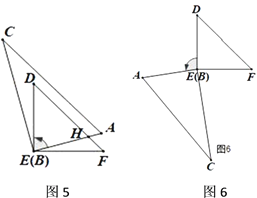
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com