
【题目】如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当t=0.5时,求线段QM的长;
(2)当M在AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形?若可以,请求t的值;若不可以,请说明理由.
(3)当t>2时,连接PQ交线段AC于点R.请探究![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.



【答案】(1)QM=1;(2)t=1或![]() 或4;(3)
或4;(3)![]() 为定值,
为定值, ![]() .
.
【解析】试题分析:(1)过点C作CF⊥AB于F,利用直线平行得出Rt△AQM∽Rt△ACF,再利用对应边的比值相等求出即可;
(2)由于∠DCA为锐角,故有三种情况:
①当∠CPQ=90°时,点P与点E重合,可得DE+CP=CD,从而可求t;②当∠PQC=90°时,如备用图1,容易证出Rt△PEQ∽Rt△QMA,再利用比例线段,结合EQ=EM﹣QM =4-2t,可求t;③当P在AD上时,∠PCQ=90°,此时PD=CD,代入即可求出t的值;
(3)当t>2时,如备用图2,先证明四边形AMQP为矩形,再利用平行线分线段成比例定理的推论可得△CRQ∽△CAB,再利用比例线段可求![]() .
.
试题解析:
解:(1)过点C作CF⊥AB于F,则四边形AFCD为矩形.
∴CF=4,AF=2,
此时,Rt△AQM∽Rt△ACF,
∴![]() ,
,
即![]() ,
,
∴QM=1;
(2)根据题意可得当0≤t≤2时,以C、P、Q为顶点可以构成三角形为直角三角形,故有三种情况:
①当∠CPQ=90°时,点P与点E重合,此时DE+CP=CD,即t+t=2,∴t=1;
②当∠PQC=90°时,
如备用图1,此时Rt△PEQ∽Rt△QMA,
∴![]() ,
,
由(1)知,EQ=EM﹣QM=4﹣2t,
而PE=PC﹣CE=PC﹣(DC﹣DE)=t﹣(2﹣t)=2t﹣2,
∴![]() ,
,
∴t=![]() ;
;
③当P在AD上时,∠PCQ=90°,此时PD=CD,所以t-2=2 ,所以t=4;
综上所述,t=1或![]() 或4;
或4;
(3)![]() 为定值,
为定值,
当t>2时,如备用图2,PA=DA﹣DP=4﹣(t﹣2)=6﹣t,
由(1)得,BF=AB﹣AF=4,∴CF=BF,∴∠CBF=45°,∴QM=MB=6﹣t,∴QM=PA,
∵AB∥DC,∠DAB=90°,∴四边形AMQP为矩形,∴PQ∥AB,∴△CRQ∽△CAB,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
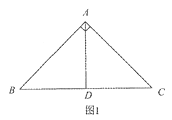
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需440元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共24个,且购买篮球的个数大于足球个数的2倍,购买球的总费用不超过2220元,问该学校有哪几种不同的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=3x2+1和y=3(x﹣1)2 , 以下说法: ①它们的图象都是开口向上;
②它们的对称轴都是y轴,顶点坐标都是原点(0,0);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们的开口的大小是一样的.
其中正确的说法有( )
A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
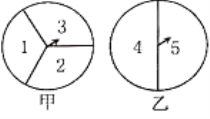
【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M和点P(点P在M内部或M上),给出如下定义:
中的图形M和点P(点P在M内部或M上),给出如下定义:
如果图形M上存在点Q,使得![]() ,那么称点P为图形M的和谐点.
,那么称点P为图形M的和谐点.
已知点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)在点![]() ,
,![]() ,
,![]() 中,矩形
中,矩形![]() 的和谐点是_________________;
的和谐点是_________________;
(2)如果直线![]() 上存在矩形
上存在矩形![]() 的和谐点P,求出点P的横坐标t的取值范围;
的和谐点P,求出点P的横坐标t的取值范围;
(3)如果直线![]() 上存在矩形
上存在矩形![]() 的和谐点E,F,使得线段
的和谐点E,F,使得线段![]() 上的所有点(含端点)都是矩形
上的所有点(含端点)都是矩形![]() 的和谐点,且
的和谐点,且![]() ,求出b的取值范围.
,求出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com