
ЁОЬтФПЁПЮЪЬтЬНОПЃК
аТЖЈвхЃК
НЋвЛИіЦНУцЭМаЮЗжЮЊУцЛ§ЯрЕШЕФСНВПЗжЕФжБЯпНазіИУЦНУцЭМаЮЕФЁАЕШЛ§ЯпЁБЃЌЦфЁАЕШЛ§ЯпЁББЛИУЦНУцЭМаЮНиЕУЕФЯпЖЮНазіИУЦНУцЭМаЮЕФЁАЕШЛ§ЯпЖЮЁБЃЈР§ШчдВЕФжБОЖОЭЪЧдВЕФЁАЕШЛ§ЯпЖЮЁБЃЉ
НтОіЮЪЬтЃК
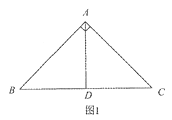
вбжЊдкRtЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=AC=2![]() .
.
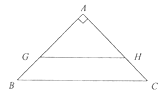
ЃЈ1ЃЉШчЭМ1ЃЌШєADЁЭBCЃЌДЙзуЮЊDЃЌдђADЪЧЁїABCЕФвЛЬѕЕШЛ§ЯпЖЮЃЌжБНгаДГіADЕФГЄЃЛ
ЃЈ2ЃЉдкЭМ2КЭЭМ3жаЃЌЗжБ№ЛГівЛЬѕЕШЛ§ЯпЖЮЃЌВЂжБНгаДГіЫќУЧЕФГЄЖШ. ЃЈвЊЧѓЃКЭМ1ЁЂЭМ2КЭЭМ3жаЕФЕШЛ§ЯпЖЮЕФГЄЖШИїВЛЯрЕШЃЉ
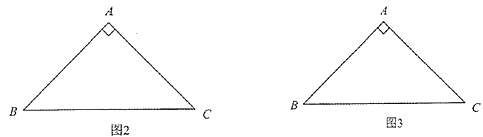
ЁОД№АИЁПЃЈ1ЃЉAD=2ЃЛЃЈ2ЃЉЗћКЯЬтвтЕФЭМаЮМћНтЮіЃЌBE=![]() ЃЌGH=2
ЃЌGH=2![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌЕзБпЩЯЕФИпЯпМДПЩЧѓЕУЃЛ
ЃЈ2ЃЉзїжаЯпBEЃЌжаЯпBEМДЮЊвЛЬѕЕШЛ§ЯпЃЌРћгУЙДЙЩЖЈРэМДПЩЧѓЕУГЄЖШЃЛ
зїGH//BCЃЌGHНЋRtЁїABCЕФУцЛ§ЗжЮЊЯрЕШЕФСНЗнЃЌдђGHМДЮЊвЛЬѕЕШЛ§ЯпЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪМДПЩЧѓЕУГЄЖШ.
ЪдЬтНтЮіЃКЃЈ1ЃЉдкRtЁїADCжаЃЌ
ЁпAC=2![]() ЃЌЁЯC=45ЁуЃЌ
ЃЌЁЯC=45ЁуЃЌ
ЁрAD=2ЃЛ
ЃЈ2ЃЉЗћКЯЬтвтЕФЭМаЮШчЯТЫљЪОЃК
EЮЊACжаЕуЃЌдђгаAE=![]() ,
,
дкRtЁїABEжаЃЌИљОнЙДЙЩЖЈРэПЩЕУBE=![]() =
=![]() ЃЛ
ЃЛ
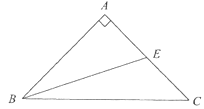
GHЁЮBCЃЌSЁїAGH=![]() SЁїABCЃЌ
SЁїABCЃЌ
ЁпGH//BCЃЌЁрЁїAGHЁзЁїABCЃЌ
Ёр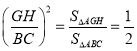 ЃЌ
ЃЌ
ЁпЁЯA=90ЁуЃЌAB=AC=![]() ЃЌЁрBC=
ЃЌЁрBC=![]() =4ЃЌ
=4ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрGH=2![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ4дТ23ШеЃЌЕк24ИіЪРНчЖСЪщШеЃЌЮЊСЫЭЦНјжаЛЊДЋЭГЮФЛЏНЬг§ЃЌгЊдьХЈгєЕФЖСЪщЗеЮЇЃЌЮвЧјФГбЇаЃОйАьСЫЁАШУЖСЪщГЩЮЊЯАЙпЃЌШУЪщЯуЦЎТњаЃдАЁБжїЬтЛюЖЏЃЌЮЊДЫЬиЮЊУПИіАрМЖЖЉЙКСЫвЛХњаТЕФЭМЪщЃЌГѕвЛФъМЖСНИіАрЖЉЙКЭМЪщЧщПіШчЯТБэЃК

РЯЩсЮФМЏЃЈЬзЃЉ | ЫФДѓУћЩЦЃЈЬзЃЉ | змБэгУЃЈдЊЃЉ | |
ГѕвЛЃЈ1ЃЉАр | 4 | 2 | 80 |
ГѕвЛЃЈ2ЃЉАр | 2 | 3 | 520 |
ЃЈ1ЃЉЧѓРЯЩсЮФМЏКЭЫФДѓУћжјУПЬзИїЪЧЖрЩйдЊЃЛ
ЃЈ2ЃЉбЇаЃзМБИдйЙКТђРЯЩсЮФМЏКЭЫФДѓУћжјЙВ10ЬзЃЌзмЗбгУВЛГЌЙ§700дЊЁЃЮЪбЇаЃгаФФМИжжЙКТђЗНАИЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЃЌAFЗжБ№ЮЊЁїABCЕФжаЯпКЭИпЃЌBEЮЊЁїABDЕФНЧЦНЗжЯпЃЎ
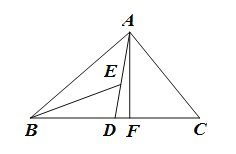
ЃЈ1ЃЉШєЁЯBED=40ЁуЃЌЁЯBAD=25ЁуЃЌЧѓЁЯBAFЕФДѓаЁЃЛ
ЃЈ2ЃЉШєЁїABCЕФУцЛ§ЮЊ40ЃЌBD=5ЃЌЧѓAFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
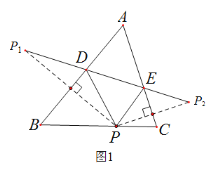
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌдкЁїABCжаЃЌЁЯA![]() ЃЌPЪЧBCБпЩЯЕФвЛЕуЃЌ
ЃЌPЪЧBCБпЩЯЕФвЛЕуЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЕуPЙигкABЁЂACЕФЖдГЦЕуЃЌСЌНс
ЪЧЕуPЙигкABЁЂACЕФЖдГЦЕуЃЌСЌНс![]() ЃЌЗжБ№НЛABЁЂACгкЕуDЁЂE.
ЃЌЗжБ№НЛABЁЂACгкЕуDЁЂE.
ЂйШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЂкЧыжБНгаДГіЁЯAгы![]() ЕФЪ§СПЙиЯЕЃК___________________________ЃЛ
ЕФЪ§СПЙиЯЕЃК___________________________ЃЛ
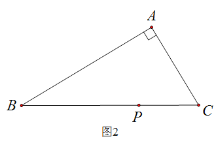
ЃЈ2ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌШєЁЯBAC![]() ЃЌгУШ§НЧАхзїГіЕуPЙигкABЁЂACЕФЖдГЦЕу
ЃЌгУШ§НЧАхзїГіЕуPЙигкABЁЂACЕФЖдГЦЕу![]() ЁЂ
ЁЂ![]() ЃЌЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЌЪдХаЖЯЕу
ЃЌЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЌЪдХаЖЯЕу![]() ЃЌ
ЃЌ![]() гыЕуAЪЧЗёдкЭЌвЛжБЯпЩЯЃЌВЂЫЕУїРэгЩ.
гыЕуAЪЧЗёдкЭЌвЛжБЯпЩЯЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЮЛХЉУёДјЩЯШєИЩЧЇПЫздВњЕФЭСЖЙНјГЧГіЪлЃЎЮЊСЫЗНБуЃЌЫћДјСЫвЛаЉСуЧЎБИгУЃЌАДЪаГЁМлЪлГівЛаЉКѓЃЌгжНЕМлГіЪлЃЌЪлГіЕФЭСЖЙЧЇПЫЪ§гыЫћЪжжаГжгаЕФЧЎЪ§ЃЈКЌБИгУСуЧЎЃЉЕФЙиЯЕЃЌШчЭМЃЌНсКЯЭМЯѓЛиД№ЯТСаЮЪЬтЃК
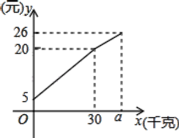
ЃЈ1ЃЉХЉУёздДјЕФСуЧЎЪЧЖрЩйЃП
ЃЈ2ЃЉЧѓГіНЕМлЧАУПЧЇПЫЕФЭСЖЙМлИёЪЧЖрЩйЃП
ЃЈ3ЃЉНЕМлКѓЫћАДУПЧЇПЫ0.4дЊНЋЪЃгрЭСЖЙЪлЭъЃЌетЪБЫћЪжжаЕФЧЎЃЈКЌБИгУСуЧЎЃЉЪЧ26дЊЃЌЪдЮЪЫћвЛЙВДјСЫЖрЩйЧЇПЫЭСЖЙЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЧѓвЛДЮКЏЪ§y=2x-2ЕФЭМЯѓl1гыy=![]() x-1ЕФЭМЯѓl2ЕФНЛЕуPЕФзјБъ.
x-1ЕФЭМЯѓl2ЕФНЛЕуPЕФзјБъ.
ЃЈ2ЃЉЧѓжБЯп![]() гы
гы![]() жсНЛЕуAЕФзјБъ; ЧѓжБЯп
жсНЛЕуAЕФзјБъ; ЧѓжБЯп![]() гыxжсЕФНЛЕуBЕФзјБъ;
гыxжсЕФНЛЕуBЕФзјБъ;
ЃЈ3ЃЉЧѓгЩШ§ЕуPЁЂAЁЂBЮЇГЩЕФШ§НЧаЮЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌEЪЧABБпЩЯвЛЕуЃЌЧвЁЯA=ЁЯEDF=60ЁуЃЌгаЯТСаНсТлЃКЂйAE=BFЃЛЂкЁїDEFЪЧЕШБпШ§НЧаЮЃЛЂлЁїBEFЪЧЕШбќШ§НЧаЮЃЛЂмЁЯADE=ЁЯBEFЃЌЦфжаНсТле§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ

A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЛЗБЃжОдИепаЛсЖдИУЪаГЧЧјЕФПеЦјжЪСПНјааЕїВщЃЌДгШЋФъ365ЬьжаЫцЛњГщШЁСЫ80ЬьЕФПеЦјжЪСПжИЪ§ЃЈAQIЃЉЪ§ОнЃЌЛцжЦГіШ§ЗљВЛЭъећЕФЭГМЦЭМБэЃЎЧыИљОнЭМБэжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
AQIжИЪ§ | жЪСПЕШМЖ | ЬьЪ§ЃЈЬьЃЉ |
0Љ50 | гХ | m |
51Љ100 | СМ | 44 |
101Љ150 | ЧсЖШЮлШО | n |
151Љ200 | жаЖШЮлШО | 4 |
201Љ300 | жиЖШЮлШО | 2 |
300вдЩЯ | бЯжиЮлШО | 2 |
ЃЈ1 ЃЉЭГМЦБэжаm= ЃЌn= ЃЎЩШаЮЭГМЦЭМжаЃЌПеЦјжЪСПЕШМЖЮЊЁАСМЁБЕФЬьЪ§еМ %ЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЌВЂЭЈЙ§МЦЫуЙРМЦИУЪаГЧЧјШЋФъПеЦјжЪСПЕШМЖЮЊЁАгХЁБКЭЁАСМЁБЕФЬьЪ§ЙВЖрЩйЬьЃП
ЃЈ3ЃЉОнЕїВщЃЌбЯжиЮлШОЕФ2ЬьЗЂЩњдкДКНкЦкМфЃЌШМЗХбЬЛЈБЌжёГЩЮЊПеЦјЮлШОЕФвЛИіживЊдвђЃЌОнДЫЃЌЧыФуЬсГівЛЬѕКЯРэЛЏНЈвщЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБНЧЬнаЮABCDжаЃЌABЁЮDCЃЌЁЯDABЃН90ЁуЃЌADЃН2DCЃН4ЃЌABЃН6ЃЎЖЏЕуMвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЃЌДгЕуAбиЯпЖЮABЯђЕуBдЫЖЏЃЛЭЌЪБЕуPвдЯрЭЌЕФЫйЖШЃЌДгЕуCбиелЯпCЃDЃAЯђЕуAдЫЖЏЃЎЕБЕуMЕНДяЕуBЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЕуMзїжБЯпlЁЮADЃЌгыЯпЖЮCDЕФНЛЕуЮЊEЃЌгыелЯпAЃCЃBЕФНЛЕуЮЊQЃЎЕуMдЫЖЏЕФЪБМфЮЊtЃЈУыЃЉЃЎ
ЃЈ1ЃЉЕБtЃН0.5ЪБЃЌЧѓЯпЖЮQMЕФГЄЃЛ
ЃЈ2ЃЉЕБMдкABЩЯдЫЖЏЪБЃЌЪЧЗёПЩвдЪЙЕУвдCЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЮЊжБНЧШ§НЧаЮЃПШєПЩвдЃЌЧыЧѓtЕФжЕЃЛШєВЛПЩвдЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЕБtЃО2ЪБЃЌСЌНгPQНЛЯпЖЮACгкЕуRЃЎЧыЬНОП![]() ЪЧЗёЮЊЖЈжЕЃЌШєЪЧЃЌЪдЧѓетИіЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёЮЊЖЈжЕЃЌШєЪЧЃЌЪдЧѓетИіЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ



ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com