
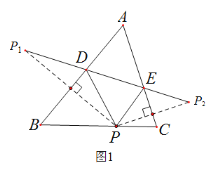
【题目】(1)如图1,在△ABC中,∠A![]() ,P是BC边上的一点,
,P是BC边上的一点,![]() ,
,![]() 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结![]() ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E.
①若![]() ,求
,求![]() 的度数;
的度数;
②请直接写出∠A与![]() 的数量关系:___________________________;
的数量关系:___________________________;
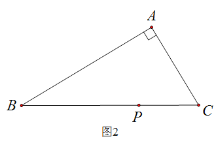
(2)如图2,在△ABC中,若∠BAC![]() ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点![]() 、
、![]() ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点![]() ,
,![]() 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由.
【答案】(1)64°;(2)∠DPE=180°-2∠A;(3)在.
【解析】(1)①由轴对称的性质以及四边形内角和为360°可得:∠DPP1+∠DPE+∠EPP2+∠A=180°(i),由三角形外角的性质以及三角形内角和为180°得到2∠DPP1+∠DPE+2∠EPP2=180°(ii),解方程组即可得到结论![]()
(2)由①得∠DPP1+∠DPE+∠EPP2+∠A=180°(i),2∠DPP1+∠DPE+2∠EPP2=180° (ii),解方程组即可得到结论.
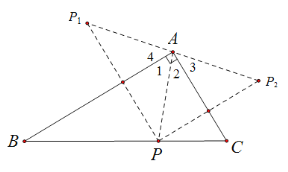
(3)连接AP、AP1、AP2.根据轴对称的性质,可得:∠4=∠1,∠3=∠2, 由∠BAC=90°,得到∠3+∠4=90°,即有∠1+∠2+∠3+∠4=180°,从而得到结论.
(1)①∵点P、点P1关于直线AB对称,点P、点P2关于直线AC对称,∴PD=P1D,PE=P2E,∴∠P1=∠DPP1,∠P2=∠EPP2,∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,∠DPP1+∠DPE+∠EPP2+∠A=180°(i)
∵2∠DPP1+∠DPE+2∠EPP2=180° (ii)
(ii)—(i)得:∠DPP1+∠EPP2=∠A,
又∵∠A=58°,∴∠DPP1+∠EPP2=58°,
∴∠DPE=64°![]()
(2)∠DPE=180°-2∠A .理由如下:
由①得:∠DPP1+∠DPE+∠EPP2+∠A=180°(i)
2∠DPP1+∠DPE+2∠EPP2=180° (ii)
(i)×2-(ii)得:2∠A-∠DPE=180°,
∴∠DPE=180°-2∠A .
(3)点P1,A,P2在同一条直线上.理由如下:
连接AP、AP1、AP2.
根据轴对称的性质,可得:∠4=∠1,∠3=∠2,
∵∠BAC=90°,即∠1+∠2=90°,
∴∠3+∠4=90°,
∴∠1+∠2+∠3+∠4=180°,
即∠P1AP2=180°,
∴点P1 、A、P2在同一条直线上.


科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,
中,![]() .射线
.射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,同点
的速度运动,同点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]() ;
;

(1)连接![]() ,当
,当![]() 经过
经过![]() 边的中点
边的中点![]() 时,求证:
时,求证:![]() ;
;
(2)求当![]() 为何值,四边形
为何值,四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=115°,那么∠BFD的度数是
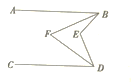
A.62°B.64°C.57.5°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
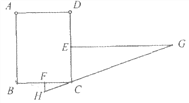
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长9里,城墙BC长7里,东门所在的点E,南门所在的点F分别是CD,BC的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=________里.
查看答案和解析>>
科目:初中数学 来源: 题型:
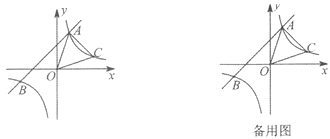
【题目】已知:如图,一次函数y=x+2的图象与反比例函数y=![]() 的图象交于A、B两点,且点A的坐标为(1,m).
的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)点C(n,1)在反比例函数y=![]() 的图象上,求△AOC的面积.
的图象上,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
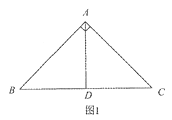
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
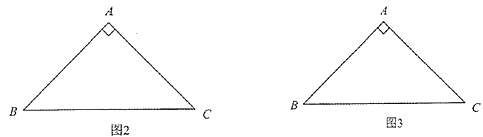
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名同学调查了全班![]() 名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
最喜欢的节目类别 | 划记 | 人数 | 百分数(%) |
相声 | 正 |
|
|
小品 | 正正正一 |
|
|
歌曲 | 正正 |
|
|
舞蹈 | 正一 |
|
|
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.相声B.小品C.歌曲D.舞蹈
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需440元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共24个,且购买篮球的个数大于足球个数的2倍,购买球的总费用不超过2220元,问该学校有哪几种不同的购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com