
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)详见解析;(2)30°;(3)![]() .
.
【解析】试题分析:(1)连接![]() 圆的半径相等和已知条件证明
圆的半径相等和已知条件证明![]() ,即可证明
,即可证明![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 首先证明
首先证明![]() 是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠
是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠![]() 的度数;
的度数;
(3)过点O作OG⊥AB于点G,得到AG=BG,在![]() 中
中![]() 设DE=5x,则AE=13x,AD=12x,AO=24x,把
设DE=5x,则AE=13x,AD=12x,AO=24x,把![]() 表示出来,在
表示出来,在![]() 中,用三角函数的知识列出方程,解出
中,用三角函数的知识列出方程,解出![]() 得值,即可求出半径.
得值,即可求出半径.
试题解析:(1)证明:连接OB,
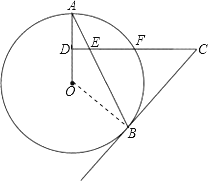
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC.
又∵CD⊥OA.
![]()
![]()
∴OB⊥BC
∴BC是![]() 的切线.
的切线.
(2)连接OF,AF,BF,
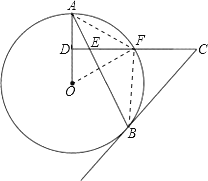
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
![]()
![]()
(3)连接OF,AF,
∵DA=
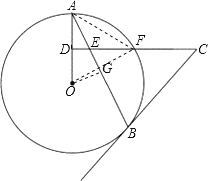
∴AF=OF=OA,
过点O作OG⊥AB于点G,得到AG=BG,
在![]() 中
中![]()
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,∴AB=10+13x.
则![]()
又∵![]() 中,
中, ![]() 则
则![]()
则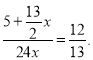
解得![]()
![]()


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:BH∥DG;
(2)求证:△BEH≌△DFG;
(3)若AB=6 cm,BC=8 cm.
①BF=________cm;
②求线段CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
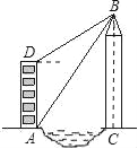
【题目】如图,小莉的家在锦江河畔的电梯公寓AD内,她家的河对岸新建了一座大厦BC,为了测量大厦的高度,小莉在她家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦顶部B的仰角为30°,已知电梯公寓高82米,请你帮助小莉计算出大厦的高度BC及大厦与电梯公寓间的距离AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 、
、![]() 为直线
为直线![]() 上两点,且满足
上两点,且满足![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
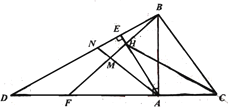
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 是线段
是线段![]() 上的动点,连
上的动点,连![]() 并延长交
并延长交![]() 于
于![]() ,当
,当![]() 在线段
在线段![]() 的什么位置上时,
的什么位置上时,![]() ?请说明理由;
?请说明理由;
(3)在(2)的结论下,判断线段![]() 、
、![]() 、
、![]() 的数量关系.请说明理由.
的数量关系.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
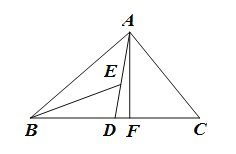
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
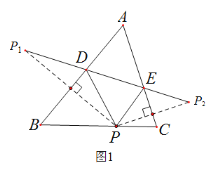
【题目】(1)如图1,在△ABC中,∠A![]() ,P是BC边上的一点,
,P是BC边上的一点,![]() ,
,![]() 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结![]() ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E.
①若![]() ,求
,求![]() 的度数;
的度数;
②请直接写出∠A与![]() 的数量关系:___________________________;
的数量关系:___________________________;
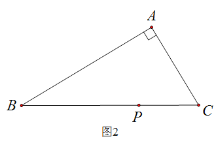
(2)如图2,在△ABC中,若∠BAC![]() ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点![]() 、
、![]() ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点![]() ,
,![]() 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)求一次函数y=2x-2的图象l1与y=![]() x-1的图象l2的交点P的坐标.
x-1的图象l2的交点P的坐标.
(2)求直线![]() 与
与![]() 轴交点A的坐标; 求直线
轴交点A的坐标; 求直线![]() 与x轴的交点B的坐标;
与x轴的交点B的坐标;
(3)求由三点P、A、B围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是作一个角的角平分线的方法:以![]() 的顶点
的顶点![]() 为圆心,以任意长为半径画弧,分别交
为圆心,以任意长为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作画弧,两条弧交于点
长为半径作画弧,两条弧交于点![]() ,作射线
,作射线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com